[Chinese ver]
4. Median of Two Sorted Arrays
這里有兩個(gè)有序數(shù)組nums1和nums2,他們各自的大小為m和n.
找到這兩個(gè)數(shù)組的中間值浩聋,總的時(shí)間復(fù)雜度應(yīng)該為O(log (m+n)).
Example 1:
nums1 = [1, 3]
nums2 = [2]
中間值是 2.0
Example 2:
nums1 = [1, 2]
nums2 = [3, 4]
中間值是 (2 + 3)/2 = 2.5
方法一:
首先嘗試了一種比較笨的方法
public class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
//需要幾個(gè)數(shù)值
int needNum = 0;
//數(shù)值位置
int needIndex = 0;
//中間值
double median = 0;
int big = 0;
int stand = 0;
//合成的數(shù)組
int[] insertnum ;
int m = nums1.length;
int n = nums2.length;
if((m+n)%2==0){
needNum = 2;
needIndex = (m+n)/2-1;
}else{
needNum=1;
needIndex = (m+n)/2;
}
insertnum = new int[m+n];
//nums1的下標(biāo)
int j =0;
//nums2的下標(biāo)
int k = 0;
for(int i =0;i<m+n;i++){
if(k==n){
insertnum[i] = nums1[j];
j++;
}
else if(j==m){
insertnum[i] = nums2[k];
k++;
}else if(nums1[j]>nums2[k]){
insertnum[i] = nums2[k];
k++;
}else{
insertnum[i] = nums1[j];
j++;
}
}
if(needNum == 1){
median = Double.valueOf(insertnum[needIndex]);
}else{
median = Double.valueOf(insertnum[needIndex]+insertnum[needIndex+1]) /2.0;
}
return median;
}
}
順便提一下凶赁,這個(gè)方法經(jīng)常無法通過咧栗,應(yīng)該是時(shí)間復(fù)雜度過高的原因吧。
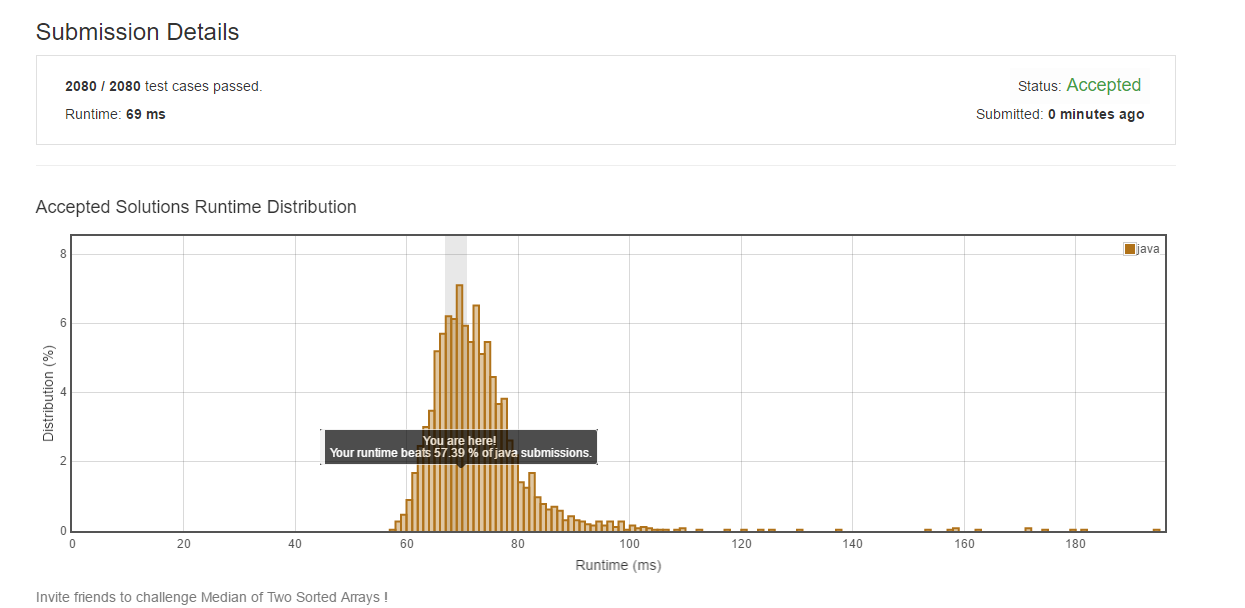
分析
這個(gè)方法的原理很簡單虱肄,首先將兩個(gè)數(shù)組個(gè)數(shù)和是奇數(shù)和偶數(shù)的情況所需的取值個(gè)數(shù)以及中間值計(jì)算方法得出致板。然后將兩個(gè)數(shù)組按照從小到大的順序合并成一個(gè)數(shù)組,最后根據(jù)前面得到的中間數(shù)的計(jì)算方法得出中間值咏窿。
時(shí)間復(fù)雜度 : O(m+n) 斟或。
空間復(fù)雜度 : O(m+n) .
這個(gè)方法可以在做一個(gè)優(yōu)化,如下:
public class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int needNum = 0;
int needIndex = 0;
double median = 0;
int big = 0;
int stand = 0;
int[] insertnum ;
int m = nums1.length;
int n = nums2.length;
if((m+n)%2==0){
needNum = 2;
needIndex = (m+n)/2-1;
}else{
needNum=1;
needIndex = (m+n)/2;
}
insertnum = new int[(m+n)/2+1];
int j =0;
int k = 0;
for(int i =0;i<m+n;i++){
if(k==n){
insertnum[i] = nums1[j];
j++;
}
else if(j==m){
insertnum[i] = nums2[k];
k++;
}else if(nums1[j]>nums2[k]){
insertnum[i] = nums2[k];
k++;
}else{
insertnum[i] = nums1[j];
j++;
}
if (i >= needIndex ){
if (needNum == 1){
median = Double.valueOf(insertnum[needIndex]);
return median;
}else{
if (i == needIndex+1){
median = Double.valueOf(insertnum[needIndex]+insertnum[needIndex+1]) /2.0;
return median;
}
}
}
}
return median;
}
}
分析
這個(gè)方法優(yōu)化的地方就是通過事先得到中間值的位置集嵌,在得到該位置的數(shù)值之后就不繼續(xù)往下走了萝挤。
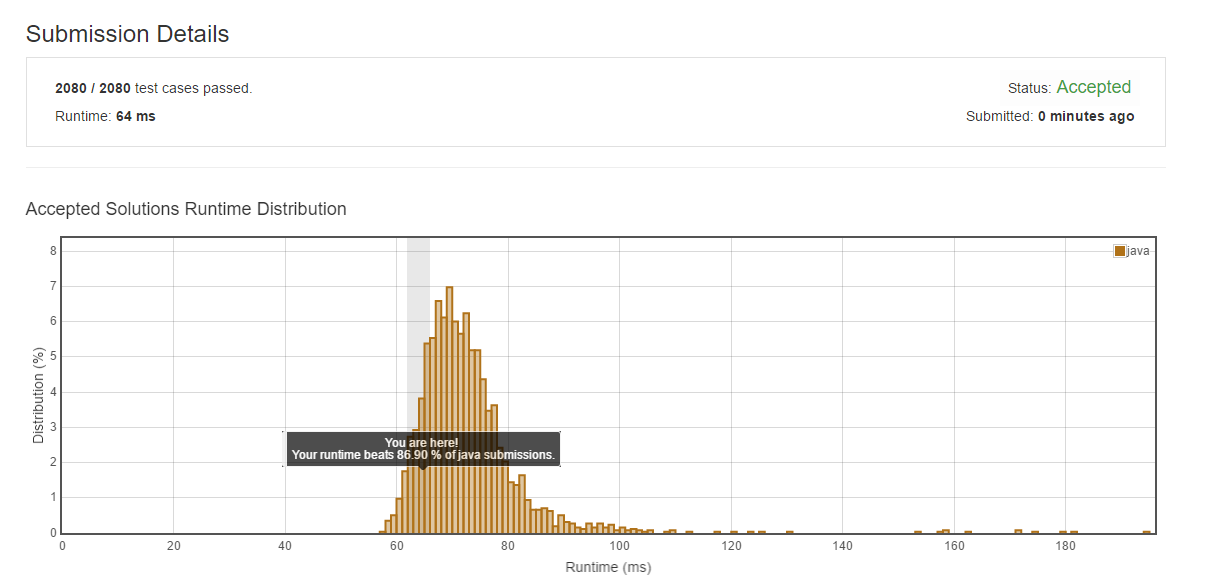
方法二:
public class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int N1 = nums1.length;
int N2 = nums2.length;
if (N1 < N2)
return findMedianSortedArrays(nums2, nums1); // Make sure A2 is the shorter one.
if (N2 == 0)
return ((double) nums1[(N1 - 1) / 2] + (double) nums1[N1 / 2]) / 2; // If A2 is empty
int lo = 0, hi = N2 * 2;
while (lo <= hi) {
int mid2 = (lo + hi) / 2; // Try Cut 2
int mid1 = N1 + N2 - mid2; // Calculate Cut 1 accordingly
double L1 = (mid1 == 0) ? Integer.MIN_VALUE : nums1[(mid1 - 1) / 2]; // Get L1, R1, L2, R2 respectively
double L2 = (mid2 == 0) ? Integer.MIN_VALUE : nums2[(mid2 - 1) / 2];
double R1 = (mid1 == N1 * 2) ? Integer.MAX_VALUE : nums1[(mid1) / 2];
double R2 = (mid2 == N2 * 2) ? Integer.MAX_VALUE : nums2[(mid2) / 2];
if (L1 > R2)
lo = mid2 + 1; // A1's lower half is too big; need to move C1 left (C2 right)
else if (L2 > R1)
hi = mid2 - 1; // A2's lower half too big; need to move C2 left.
else
return ((L1 > L2 ? L1 : L2) + (R1 > R2 ? R2 : R1)) / 2; // Otherwise, that's the right cut.
}
return -1;
}
}
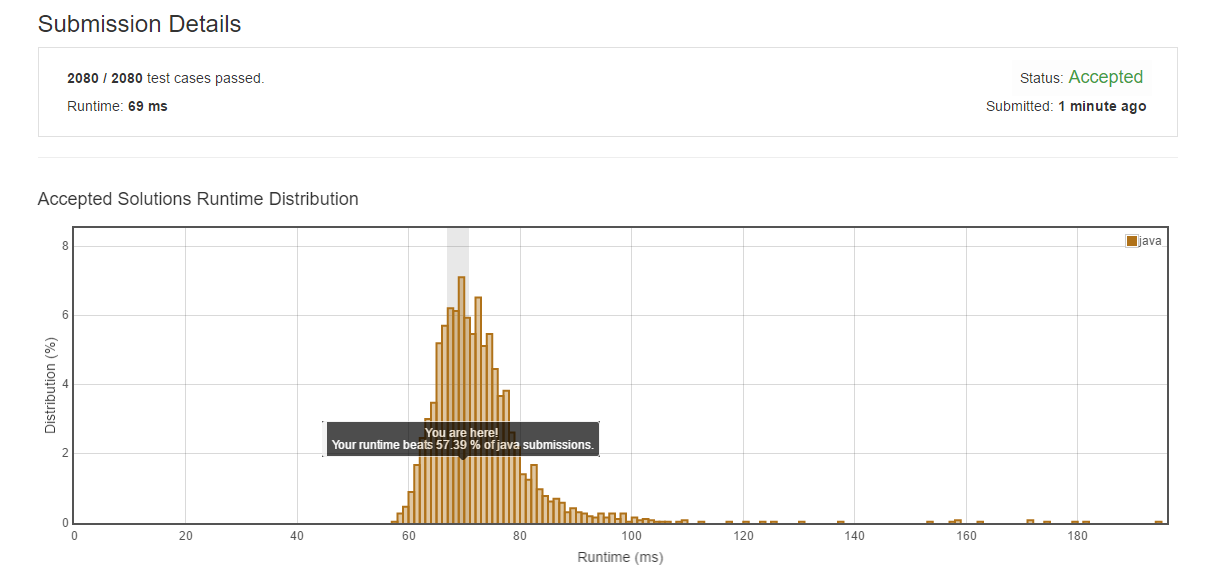
分析
這個(gè)問題比較困難,很多方法都是把他分成兩種情況根欧,奇數(shù)個(gè)和偶數(shù)個(gè)怜珍。實(shí)際上這樣有點(diǎn)復(fù)雜,我們可以把這兩個(gè)情況合并成一種情況咽块。
首先绘面,我們來重新定義一下'median'的含義:
“如果我們把一個(gè)有序的array分成兩個(gè)等長的部分,那么median就是比較小的那一部分的最大值和比較大的那一部分的最小值的平均值侈沪。即劃分線兩邊的數(shù)揭璃。”
比如[1,2],我們的分割線就應(yīng)該在1亭罪,2之間瘦馍,[1 | 2],結(jié)果是(1 + 2)/2.0 = 1.5。
同理应役,如果是兩個(gè)有序的數(shù)組情组,那么我們只需要保證兩個(gè)數(shù)組劃分線右側(cè)的數(shù)都大于左側(cè)的數(shù),并且兩個(gè)數(shù)組左側(cè)數(shù)字個(gè)數(shù)的和等于右側(cè)數(shù)字個(gè)數(shù)的和箩祥。
我們使用‘|’來代表分割線院崇,(n|n)來表示分割線正好在某個(gè)數(shù)字n上。
比如[1 2 3],得到的分割后的數(shù)組像這樣[1 (2|2) 3],z中間值就是(2+2)/2.0 = 2
我們使用L代表分割線左邊的數(shù)袍祖,R代表分割線右邊的數(shù)底瓣。
可以觀察到左邊的數(shù)和右邊的數(shù)有這樣的規(guī)律。
N Index of L / R
1 0 / 0
2 0 / 1
3 1 / 1
4 1 / 2
5 2 / 2
6 2 / 3
7 3 / 3
8 3 / 4
可以得到 L = (N-1)/2, R = N/2. 中間值為(L + R)/2 = (A[(N-1)/2] + A[N/2])/2
為了更方便的計(jì)算兩個(gè)數(shù)組的情況蕉陋,我們添加一些空位在數(shù)字之間捐凭。用'#'代表拨扶,用'position'來表示增加空格后的位置信息。
[1 2] -> [# 1 # 2 #] (N=2)
position 0 1 2 3 4 (N_Position = 5)
[3 4] -> [# 3 # 4 #] (N=2)
position 0 1 2 3 4 (N_Position = 5)
可以看出N_Position = 2N+1.所以分割線是在N茁肠,index(L) = (CutPosition-1)/2, index(R) = (CutPosition)/2.
當(dāng)我們分割這兩個(gè)數(shù)組的時(shí)候要注意患民,總共有2N1+2N2+2的位置,所以垦梆,分割線的每一邊都要有N1+N2個(gè)位置匹颤,剩下的2個(gè)就是切線的位置,所以當(dāng)我們A2分割線在 C2 = K , 那么A1的分割線就必須要在C1 = N1 + N2 - k. 比如, C2 = 2, 那么 C1 = 2 + 2 - C2 = 2.
[# 1 | 2 #]
[# 3 | 4 #]
現(xiàn)在我們有了兩個(gè)L和兩個(gè)R奶赔。
L1 = A1[(C1-1)/2]; R1 = A1[C1/2];
L2 = A2[(C2-1)/2]; R2 = A2[C2/2];
即
L1 = A1[(2-1)/2] = A1[0] = 1; R1 = A1[2/2] = A1[1] = 2;
L2 = A2[(2-1)/2] = A2[0] = 3; R2 = A1[2/2] = A1[1] = 4;
那么我們要怎么判斷這個(gè)分割線是不是符合規(guī)則的呢惋嚎?我們只要左邊的數(shù)字都小于右邊的數(shù)字。首先這兩個(gè)數(shù)組都是有序的站刑,所以L1,L2是左半邊數(shù)組里最大的數(shù),R1,R2是右半邊數(shù)組里最小的數(shù)鼻百,L1<=R1.L2<=R2.
所以我們只要判斷L1<=R2,L2<=R1就可以了绞旅。
現(xiàn)在我們用簡單的二分法查找就可以得到答案了。
如果L1>R2,代表A1左邊有過多較大的數(shù)字温艇,我們必須把C1往左移因悲,同時(shí)需要把C2往右移。
如果L2>R1,代表A2左邊有過多較大的數(shù)字勺爱,我們必須把C2往左移晃琳,同時(shí)需要把C1往右移。
反之則相反琐鲁。
當(dāng)我們找到正確的分割線位置的時(shí)候卫旱,中間值 = (max(L1, L2) + min(R1, R2)) / 2。
1.因?yàn)镃1和C2可以根據(jù)彼此的值互相推斷围段,我們可以使用較短的數(shù)組(設(shè)為A2)并且只移動(dòng)C2顾翼,然后計(jì)算出C1。這樣我們的時(shí)間復(fù)雜度就是O(log(min(N1, N2)))
2.只有在極限的條件下分割線會(huì)在0,或者2N的index奈泪。比如适贸,C2=2N2,R2 = A2[2*N2/2] = A2[N2].這種情況下他有一邊是沒有數(shù)值的,我們可以把它當(dāng)成是極大或者極小涝桅,L = INT_MIN 拜姿,R = INT_MAX.
時(shí)間復(fù)雜度 : O(log(min(m,n))) 。m,n是兩個(gè)數(shù)組的長度冯遂。
空間復(fù)雜度 : O(1) .
方法三:
public class Solution {
public double findMedianSortedArrays(int A[], int B[]) {
int n = A.length;
int m = B.length;
// the following call is to make sure len(A) <= len(B).
// yes, it calls itself, but at most once, shouldn't be
// consider a recursive solution
if (n > m)
return findMedianSortedArrays(B, A);
// now, do binary search
int k = (n + m - 1) / 2;
int l = 0, r = Math.min(k, n); // r is n, NOT n-1, this is important!!
while (l < r) {
int midA = (l + r) / 2;
int midB = k - midA;
if (A[midA] < B[midB])
l = midA + 1;
else
r = midA;
}
// after binary search, we almost get the median because it must be between
// these 4 numbers: A[l-1], A[l], B[k-l], and B[k-l+1]
// if (n+m) is odd, the median is the larger one between A[l-1] and B[k-l].
// and there are some corner cases we need to take care of.
int a = Math.max(l > 0 ? A[l - 1] : Integer.MIN_VALUE, k - l >= 0 ? B[k - l] : Integer.MIN_VALUE);
if (((n + m) & 1) == 1)
return (double) a;
// if (n+m) is even, the median can be calculated by
// median = (max(A[l-1], B[k-l]) + min(A[l], B[k-l+1]) / 2.0
// also, there are some corner cases to take care of.
int b = Math.min(l < n ? A[l] : Integer.MAX_VALUE, k - l + 1 < m ? B[k - l + 1] : Integer.MAX_VALUE);
return (a + b) / 2.0;
}
}
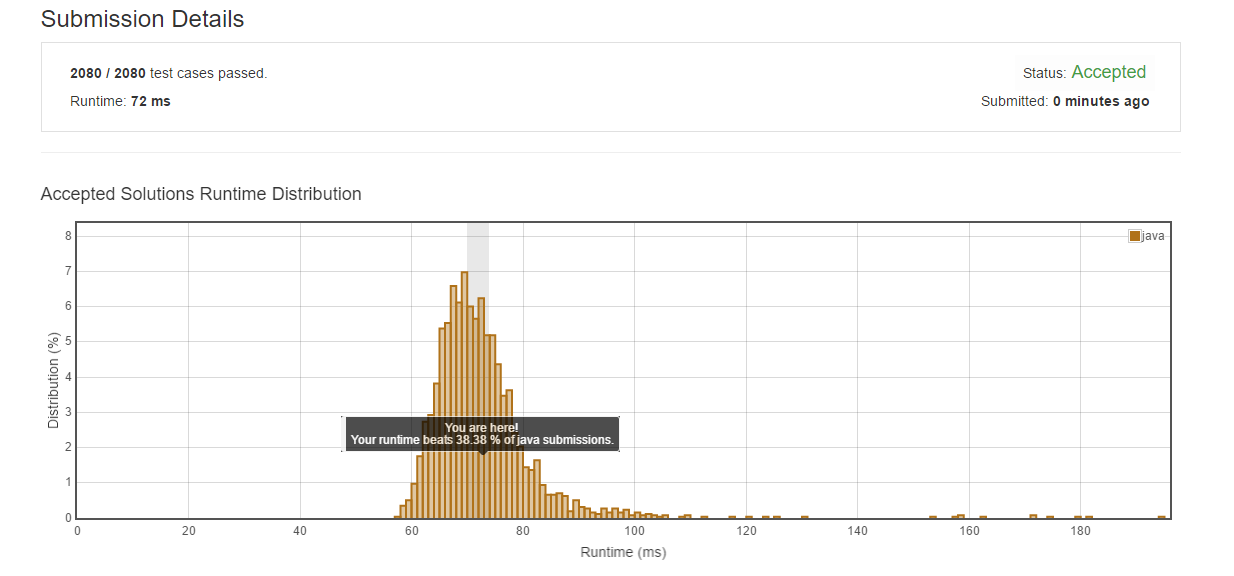
分析
這個(gè)方法的原理和上一個(gè)方法是大致相同的蕊肥。
時(shí)間復(fù)雜度 : O(log(min(m,n))) 。m,n是兩個(gè)數(shù)組的長度债蜜。
空間復(fù)雜度 : O(1) .
方法四:
public class Solution {
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length, n = B.length;
int l = (m + n + 1) / 2;//position of l element (not the index)
int r = (m + n + 2) / 2;//position of r element (not the index)
return (getkth(A, 0, B, 0, l) + getkth(A, 0, B, 0, r)) / 2.0;
}
public double getkth(int[] A, int aStart, int[] B, int bStart, int k) {
//when the start position is bigger than A.length -1 ,means the median doesn't in the A.
if (aStart > A.length - 1) return B[bStart + k - 1];
if (bStart > B.length - 1) return A[aStart + k - 1];
if (k == 1) return Math.min(A[aStart], B[bStart]);
int aMid = Integer.MAX_VALUE, bMid = Integer.MAX_VALUE;
if (aStart + k/2 - 1 < A.length) aMid = A[aStart + k/2 - 1];
if (bStart + k/2 - 1 < B.length) bMid = B[bStart + k/2 - 1];
if (aMid < bMid)
return getkth(A, aStart + k/2, B, bStart, k - k/2);// Check: aRight + bLeft
else
return getkth(A, aStart, B, bStart + k/2, k - k/2);// Check: bRight + aLeft
}
}
分析
這個(gè)方法的原理是這樣的晴埂,從兩個(gè)數(shù)組中間值開始通過遞歸對(duì)比究反,每次排除一半的選項(xiàng)。如果A的中間值小于B的中間值則保留a的右側(cè)數(shù)字和b的左側(cè)數(shù)字儒洛。反之相反精耐。然后得到l和r位置的數(shù)字,再相加除以2即可。需要注意的是這里的l和r不是index琅锻,不是從零開始的卦停。如果兩個(gè)數(shù)組的長度的和是奇數(shù)的話l和r是相同的,偶數(shù)則不同恼蓬。
時(shí)間復(fù)雜度 : O(log(m + n))
空間復(fù)雜度 : O(1)
如果你有更好的辦法或者對(duì)我這里的描述有其他看法惊完,請(qǐng)聯(lián)系我。謝謝