看了一本叫swift函數(shù)式編程的書抄淑，每一章就問(wèn)題引入討論了一下這個(gè)思想刻剥，我們來(lái)自己理解一下育灸；首先上圖腻窒，以及寫一下傳統(tǒng)做法；
首先我們按照書中的定義
typealias Position = CGPoint
typealias Distance = CGFloat
不懂typealias的請(qǐng)自行查閱磅崭；
我們總是這樣做
-
圖1所示儿子，我們現(xiàn)在要表示一個(gè)未知點(diǎn)point是否在圖中黑色圈圈內(nèi)，很自然的砸喻，我們傳入point參數(shù)柔逼，返回一個(gè)bool值，來(lái)解決這個(gè)問(wèn)題割岛，通常我們都會(huì)這樣思考愉适；
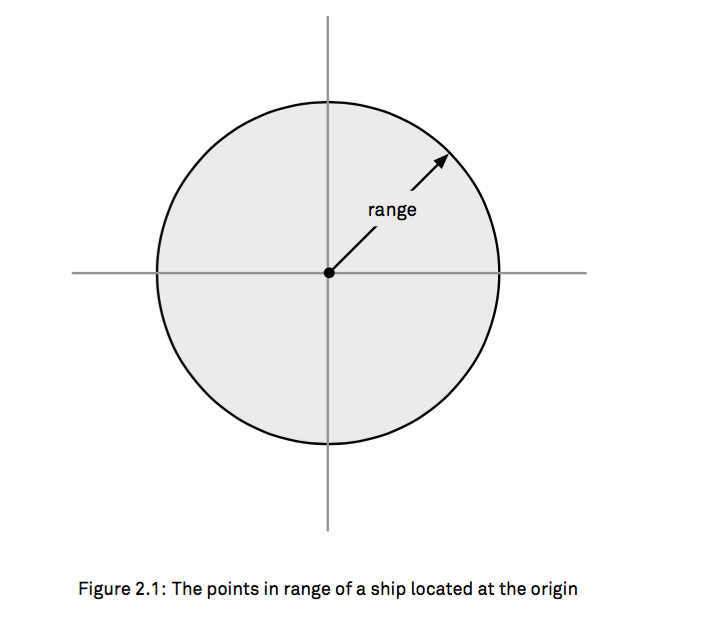inRange1
func inRange1(target: Position, range: Distance) -> Bool {
return sqrt(target.x * target.x + target.y * target.y) <= range
}
-
那么如果我們的圓心不在(0,0)點(diǎn)呢，需要做坐標(biāo)系仿射變換（線性變換加上一個(gè)平移變換）對(duì)吧癣漆，或者理解仿射有點(diǎn)吃力维咸，我們只做平移變換，就是說(shuō)現(xiàn)在我們?cè)c(diǎn)不是(0,0)了：
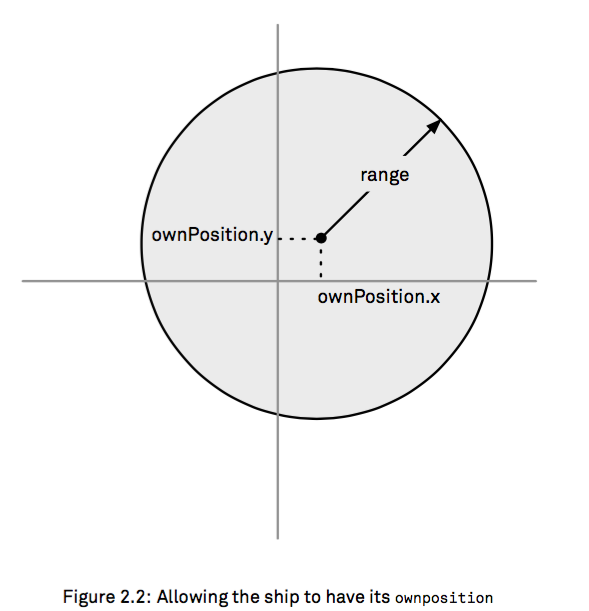inRange2
func inRange2(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(pow(dx, 2.0) + pow(dy, 2.0))
return targetDistance <= range
}
其實(shí)就是空間中的兩個(gè)點(diǎn)得出一個(gè)相對(duì)距離惠爽，也很簡(jiǎn)單對(duì)吧癌蓖，我們繼續(xù)；
-
現(xiàn)在我們又有新需求了婚肆，我們要挖去中間的這個(gè)圓租副，因?yàn)槲覀兊狞c(diǎn)現(xiàn)在要在這個(gè)環(huán)上運(yùn)動(dòng)了：
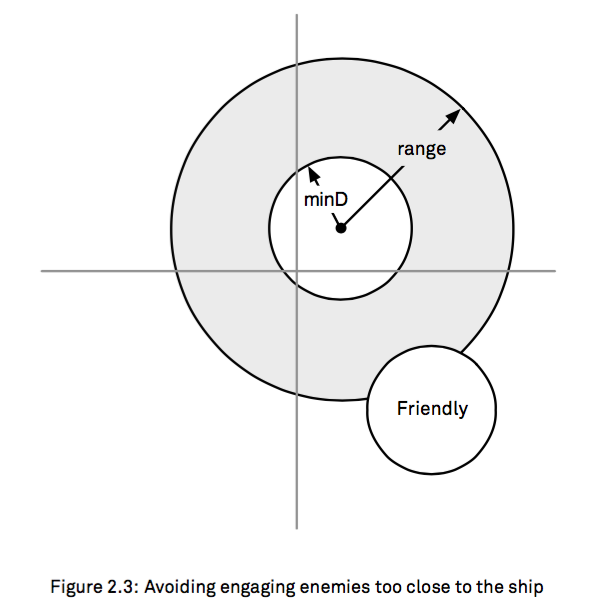inRange34
let minimumDistance: Distance = 2.0
func inRange3(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(pow(dx, 2.0) + pow(dy, 2.0))
return targetDistance <= range && targetDistance >= minimumDistance
}
就是需要我們挖去以原點(diǎn)為中心，半徑為minimumDistance的圓旬痹，也還好附井；
- 我們還要考慮如果有一個(gè)圓，讓這個(gè)圓在小圓環(huán)之外两残；
如上圖中Friendly所示永毅；
func inRange4(target: Position, ownPosition: Position, friendly:Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(dx * dx + dy * dy)
let friendlyDx = friendly.x - target.x
let friendlyDy = friendly.y - target.y
let friendlyDistance = sqrt(pow(friendlyDx, 2.0) + pow(friendlyDy, 2.0))
return targetDistance <= range
&& targetDistance >= minimumDistance
&& friendlyDistance >= minimumDistance
}
我們還可以這樣做
的確如書上所說(shuō)，我做了好多重復(fù)的工作人弓，而且從代碼復(fù)制粘貼的情況來(lái)看沼死，我似乎做了不少工作；太你太臃腫了崔赌，需要重構(gòu)意蛀！
于是我們定義了這樣一個(gè)關(guān)系耸别，它是一個(gè)關(guān)系，也是一個(gè)值县钥，作者說(shuō)函數(shù)要當(dāng)作是值來(lái)看待的秀姐；
typealias Region = (Position) -> Bool
理解起來(lái)也很容易：我是一個(gè)函數(shù)，我接受一個(gè)參數(shù)若贮，你可以將Position的點(diǎn)讓我來(lái)幫你驗(yàn)證省有，如果你通過(guò)我的驗(yàn)證，那你就是我要表達(dá)的Region谴麦，我會(huì)告訴你你的參數(shù)是不是我要的結(jié)果蠢沿；
很順暢對(duì)吧！接下來(lái)我們用它來(lái)寫幾個(gè)函數(shù)：
- inRange1重寫
func circle(radius: Distance) -> Region {
return { position in
sqrt(pow(position.x, 2.0) + pow(position.y, 2.0)) <= radius //這不加 return 竟然也可以
}
}
- inRange2重寫匾效，平移變換圓
func shift(offset: Position, region: @escaping Region) -> Region {
return { position in
return region(Position(x: position.x + offset.x, y: position.y + offset.y))
}
}
- 寫一個(gè)不是我范圍的Region
func invert(region: @escaping Region) -> Region {
return { position in
!region(position)
}
}
- 來(lái)一個(gè)相交的區(qū)域
func intersection(region1: Region, region2: Region) -> Region {
return { point in
region1(point) && region2(point)
}
}
- 來(lái)一個(gè)并集的區(qū)域
func union(region1: Region, region2: Region) -> Region {
return { point in
region1(point) || region2(point)
}
}
- 再來(lái)一個(gè)差集
//函數(shù)表示在region中舷蟀，而屬于minusRegion的部分
func difference(region: Region, minusRegion: Region) -> Region {
return intersection(region1: region, region2: invert(region: minusRegion))
}
一時(shí)間發(fā)現(xiàn)把集合的性質(zhì)寫了一個(gè)遍，那如果把這個(gè)東西寫成一個(gè)泛型面哼，用的豈不是更多野宜？
先不考慮，我們來(lái)重新寫一下之前的那個(gè)inRange4吧魔策！
最終inRange版本
func inRange(ownPosition: Position, target: Position, friendly: Position, range: Distance) -> Bool {
//表示灰色的圓環(huán)速缨，頂點(diǎn)為(0,0)的圓環(huán)
let rangeRegion = difference(region: circle(radius: range), minusRegion: circle(radius: minimumDistance))
//發(fā)生了平移變換后的圓環(huán)
let targetRegion = shift(offset: ownPosition, region: rangeRegion)
//發(fā)生了平移變換后的朋友圈
let friendlyRegion = shift(offset: friendly, region: circle(radius: minimumDistance))
//最終結(jié)果為在目標(biāo)圓環(huán)中，而不在朋友圈的區(qū)域
let resultRegion = difference(region: targetRegion, minusRegion: friendlyRegion)
return resultRegion(target)
}
結(jié)論
我不知道這過(guò)程中我做了什么代乃，總的來(lái)說(shuō)我貌似理解的更清晰了旬牲，改天再研究吧！你有什么想法搁吓，我們可以探討一下霸！
