A題“洗個(gè)熱水澡”是一道涉及熱傳導(dǎo)的連續(xù)性問題,用到了牛頓冷卻定律漠趁、N-S方程等公式定理進(jìn)行模型的建立,同時(shí)利用CFD等軟件進(jìn)行流體的模擬秘狞,降低了編程建模的難度嗤疯。
為了方便討論模型,這篇論文中做了一些處理
-
做出一些假設(shè)摩桶,讓我們的關(guān)注點(diǎn)集中在問題上面
- 浴缸水是不可壓縮的非牛頓流體桥状,非牛頓流體是應(yīng)用N-S方程模擬洗澡水流動(dòng)的基礎(chǔ)
洗澡水、空氣硝清、浴缸等是保持穩(wěn)定的辅斟,如空氣密度的變化對(duì)于模型的影響可以忽略,浴缸和水的比熱的變化也是可以忽略的
整個(gè)系統(tǒng)中沒有內(nèi)能源對(duì)體系輸入能量
我們忽略輻射能的損失芦拿,根據(jù)波爾茲曼輻射率士飒,當(dāng)溫度較低時(shí),物體的輻射能很小可以忽略不計(jì)
加入的熱水溫度是保持恒定的
做一些標(biāo)記蔗崎,方便分析模型
將模型分為兩步酵幕,一步模型是持續(xù)地放水,另一步模型是間斷地放水
分析一些影響因素:如浴缸的形狀和容量缓苛,人在洗澡時(shí)的動(dòng)作等
一些標(biāo)記

goal
在我們的模型中芳撒,我們有三個(gè)目標(biāo):
- 盡可能保持溫度恒定
- 使溫度保持在初始條件下
- 減少水的浪費(fèi)
模型一:持續(xù)的加水
1.首先假設(shè)浴缸的形狀是一個(gè)長(zhǎng)方體:

由于流體是穩(wěn)定連續(xù)流進(jìn)流出的,因此我們提出一個(gè)連續(xù)性方程:
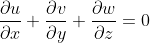
由于流體不可壓縮,應(yīng)用N-S方程:
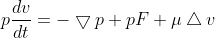
由于系統(tǒng)沒有外力作用笔刹,因此將上述方程轉(zhuǎn)化為

同時(shí)我們還要考慮到熱量在體系中傳輸?shù)挠绊懧辏虼嗽偌由蠠崃總鬏斘⒎址匠蹋?/p>
- 對(duì)于不可壓縮流體來說有:
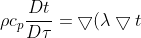+q_v + \phi) - 對(duì)于流體高速流動(dòng)或者粘性很大的流體來說,我們需要考慮\phi,在本模型中徘熔,我們可以簡(jiǎn)化為:
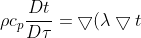)
即:
=\lambda(\frac{\partial ^2 t}{\partial x^2}+\frac{\partial ^2 t}{\partial y^2}+\frac{\partial ^2t}{\partial z^2}))
邊界情況:
流入的水的溫度是
水面和空氣之間會(huì)發(fā)生熱量交換,根據(jù)牛頓冷卻定律(牛頓冷卻定律(Newton's law of cooling):溫度高于周圍環(huán)境的物體向周圍媒質(zhì)傳遞熱量逐漸冷卻時(shí)所遵循的規(guī)律淆党。當(dāng)物體表面與周圍存在溫度差時(shí)酷师,單位時(shí)間從單位面積散失的熱量與溫度差成正比,比例系數(shù)稱為熱傳遞系數(shù)染乌。):
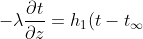)
其邊界條件為:
同時(shí)浴缸壁也會(huì)與周圍環(huán)境交換熱量山孔,因此有:
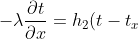)
邊界條件為: