------

二分查找基本版及其各種變形的匯總

思想:? 二分搜索的核心就是**循環(huán)結(jié)束條件**和**左右邊界迭代規(guī)則**

#### 一. 基本二分

##### 基本的二分查找

我們這個算法中使用的是前者 `[left, right]` 兩端都閉的區(qū)間盈简。**這個區(qū)間其實(shí)就是每次進(jìn)行搜索的區(qū)間**

當(dāng)然柒啤，找到了目標(biāo)值的時候可以終止

if(nums[mid] == target)

?? ? ? ? return mid;

```java

int binarySearch(int[] nums, int target) {

? ? int left = 0, right = nums.length - 1;

? ? while(left <= right) {

? ? ? ? int mid = left + (right - left) / 2;

? ? ? ? if (nums[mid] < target) {

? ? ? ? ? ? left = mid + 1;

? ? ? ? } else if (nums[mid] > target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? } else if(nums[mid] == target) {

? ? ? ? ? ? // 直接返回

? ? ? ? ? ? return mid;

? ? ? ? }

? ? }

? ? // 直接返回

? ? return -1;

}

```

#### 二. 進(jìn)階二分

##### 2.1 尋找左側(cè)邊界的二分查找

```java

int leftBound(int[] nums, int target) {

? ? int left = 0, right = nums.length - 1;

? ? while (left <= right) {

? ? ? ? int mid = left + (right - left) / 2;

? ? ? ? if (nums[mid] < target) {

? ? ? ? ? ? left = mid + 1;

? ? ? ? } else if (nums[mid] > target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? } else if (nums[mid] == target) {

? ? ? ? ? ? // 別返回挚冤，鎖定左側(cè)邊界

? ? ? ? ? ? right = mid - 1;

? ? ? ? }

? ? }

? ? // 最后要檢查 left 越界的情況

? ? if (left >= nums.length || nums[left] != target)

? ? ? ? return -1;

? ? return left;

}

```

##### 2.2 尋找右側(cè)邊界的二分查找

```java

int rightBound(int[] nums, int target) {

? ? int left = 0, right = nums.length - 1;

? ? while (left <= right) {

? ? ? ? int mid = left + (right - left) / 2;

? ? ? ? if (nums[mid] < target) {

? ? ? ? ? ? left = mid + 1;

? ? ? ? } else if (nums[mid] > target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? } else if (nums[mid] == target) {

? ? ? ? ? ? // 別返回夕冲，鎖定右側(cè)邊界

? ? ? ? ? ? left = mid + 1;

? ? ? ? }

? ? }

? ? // 最后要檢查 right 越界的情況

? ? if (right < 0 || nums[right] != target)

? ? ? ? return -1;

? ? return right;

}

```

注意點(diǎn)：**注意搜索區(qū)間 和 while的終止條件**

##### 2.3 查找最后一個等于或者小于target的元素

關(guān)鍵詞：**右邊界**

查找最后一個等于或者小于target的元素译断，也就是說如果查找target值的元素有好多個箱季，返回這些元素最右邊的元素下標(biāo)玄柏；如果沒有等于target值的元素兼呵，則返回小于target的最右邊元素下標(biāo)

```java

// 查找最后一個等于或者小于target的元素

int findLastEqualSmaller(int[] nums, int target) {

? ? int left = 0;

? ? int right = nums.length - 1;

? ? // 這里必須是 <=

? ? while (left <= right) {

? ? ? ? int mid = (left + right) / 2;

? ? ? ? if (nums[mid] > target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? }

? ? ? ? else {

? ? ? ? ? ? left = mid + 1;

? ? ? ? }

? ? }

? ? return right;? //必須返回right

}

```

##### 2.4 查找最后一個小于target的元素

返回小于target的最右邊元素下標(biāo)

```java

// 查找最后一個小于target的元素

int findLastSmaller(int[] nums, int target) {

? ? int left = 0;

? ? int right = nums.length - 1;

? ? // 這里必須是 <=

? ? while (left <= right) {

? ? ? ? int mid = (left + right) / 2;

? ? ? ? if (nums[mid] >= target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? }

? ? ? ? else {

? ? ? ? ? ? left = mid + 1;

? ? ? ? }

? ? }

? ? return right;? //必須返回right

}

```

##### 2.5 查找第一個等于或者大于target的元素

? 關(guān)鍵詞：左邊界

　查找第一個等于或者大于target 的元素畸写，也就是說如果查找target值的元素有好多個驮瞧，返回這些元素最左邊的元素下標(biāo)；如果沒有等于target值的元素枯芬，則返回大于target的最左邊元素下標(biāo)

```java

// 查找第一個等于或者大于key的元素

int findFirstEqualLarger(int[] nums, int target) {

? ? int left = 0;

? ? int right = nums.length - 1;

? ? // 這里必須是 <=

? ? while (left <= right) {

? ? ? ? int mid = (left + right) / 2;

? ? ? ? if (nums[mid] >= target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? }

? ? ? ? else {

? ? ? ? ? ? left = mid + 1;

? ? ? ? }

? ? }

? ? return left;

}

```

##### 2.6 查找第一個大于target的元素

```java

// 查找第一個大于key的元素

int findFirstLarger(int[] nums, int target) {

? ? int left = 0;

? ? int right = nums.length - 1;

? ? // 這里必須是 <=

? ? while (left <= right) {

? ? ? ? int mid = (left + right) / 2;

? ? ? ? if (nums[mid] > target) {

? ? ? ? ? ? right = mid - 1;

? ? ? ? }

? ? ? ? else {

? ? ? ? ? ? left = mid + 1;

? ? ? ? }

? ? }

? ? return left;

}

```

第一個大于等于target 或者? 最后一個小于等于target的元素论笔，擴(kuò)展開來，

最小條件:? **第一個滿足條件的** 千所，左邊界

**案例一：阿珂吃香蕉**：找到第一個滿足條件的狂魔，比 該值大的都滿足，所以是找左邊界

滿足條件指的是：canFinish(piles, mid, H)

https://leetcode-cn.com/problems/koko-eating-bananas/

```java

public int minEatingSpeed(int[] piles, int H) {

? ? ? ? int maxSpeed = getMax(piles);

? ? ? ? int left= 1;

? ? ? ? int right = maxSpeed;

? ? ? ? while(left <= right){

? ? ? ? ? ? int mid= left +(right -left)/2;

? ? ? ? ? ? if(canFinish(piles, mid, H)){? //查找左邊界淫痰，找到第一個滿足 條件的

? ? ? ? ? ? ? ? right = mid-1;

? ? ? ? ? ? } else {

? ? ? ? ? ? ? ? left = mid + 1;

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? return left;

? ? }

? ? // 時間復(fù)雜度 O(N)

? ? boolean canFinish(int[] piles, int speed, int H) {

? ? ? ? int time = 0;

? ? ? ? for (int n : piles) {

? ? ? ? ? ? time += timeOf(n, speed);

? ? ? ? }

? ? ? ? return time <= H;

? ? }

? ? int timeOf(int n, int speed) {

? ? ? ? return (n / speed) + ((n % speed > 0) ? 1 : 0);

? ? }

? ? int getMax(int[] piles) {

? ? ? ? int max = 0;

? ? ? ? for (int n : piles)

? ? ? ? ? ? max = Math.max(n, max);

? ? ? ? return max;

? ? }

```

案例二： 給定一個包含 n + 1 個整數(shù)的數(shù)組 nums最楷， 找出重復(fù)數(shù)

滿足條件： cnt[i] > i;

```java

? ? public int findDuplicate_BinarySearch(int[] nums) {

? ? ? ? int n? = nums.length;

? ? ? ? int l =1, r = n-1;

? ? ? ? while(l <=r ){

? ? ? ? ? int mid = l + (r -l)/2;

? ? ? ? ? ? int cnt = cntLessEqual(nums, mid);

? ? ? ? ? ? if(cnt > mid){//? 查找第一個滿足條件的 ：cnt[mid] > mid的最左邊

? ? ? ? ? ? ? ? r = mid -1;

? ? ? ? ? ? } else {

? ? ? ? ? ? ? ? l = mid +1;

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? return l;

? ? }

? ? private int cntLessEqual(int[] nums, int target){

? ? ? ? int cnt = 0;

? ? ? ? for(int n:nums){

? ? ? ? ? ? if(n <= target){

? ? ? ? ? ? ? ? cnt++;

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? return cnt;

? ? }

```

#### 三. 二分查找變種總結(jié)

```java

// 這里必須是 <=

while (left <= right) {

? ? int mid = (left + right) / 2;

? ? if (array[mid] ? key) {

? ? ? ? //... right = mid - 1;

? ? }

? ? else {

? ? ? ? // ... left = mid + 1;

? ? }

}

return xxx;

```

1. 首先判斷出是返回left，還是返回right

? 因?yàn)槲覀冎雷詈筇鰓hile (left <= right)循環(huán)條件是right < left待错，且right = left - 1籽孙。最后right和left一定是卡在"邊界值"的左右兩邊，如果是比較值為key火俄，查找小于等于（或者是小于）key的元素犯建，則邊界值就是等于key的所有元素的最左邊那個，其實(shí)應(yīng)該返回left瓜客。

? 　　以數(shù)組{1, 2, 3, 3, 4, 5}為例胎挎，如果需要查找第一個等于或者小于3的元素下標(biāo)，我們比較的key值是3忆家，則最后left和right需要滿足以下條件：

? 

? 　　我們比較的key值是3犹菇，所以此時我們需要返回left

2. 判斷出比較符號

? ```java

? int mid = (left + right) / 2;

? if (array[mid] ? key) {

? ? ? //... right = xxx;

? }

? else {

? ? ? // ... left = xxx;

? }

? ```

? 　也就是這里的 if (array[mid] ? key) 中的判斷符號，結(jié)合步驟1和給出的條件芽卿，如果是查找小于等于key的元素揭芍，則知道應(yīng)該使用判斷符號>=，因?yàn)槭且祷豯eft卸例，所以如果array[mid]等于或者大于key称杨，就應(yīng)該使用>=肌毅，以下是完整代碼

? ```java

? // 查找小于等于key的元素

? int mid = (left + right) / 2;

? if (array[mid] >= key) {

? ? ? right = mid - 1;

? }

? else {

? ? ? left = mid + 1;

? }

? ```

### 另類二叉查找

https://leetcode-cn.com/problems/find-peak-element/

尋找峰值


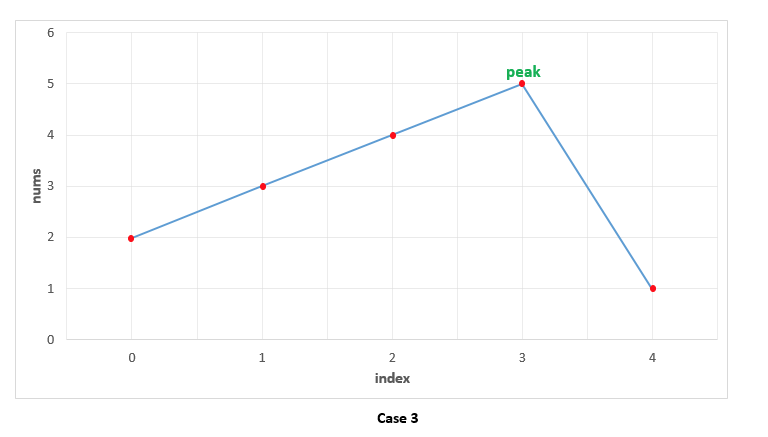
峰值元素是指其值大于左右相鄰值的元素。

給定一個輸入數(shù)組 nums姑原，其中 nums[i] ≠ nums[i+1]悬而，找到峰值元素并返回其索引。

數(shù)組可能包含多個峰值锭汛，在這種情況下笨奠，返回任何一個峰值所在位置即可。

你可以假設(shè) nums[-1] = nums[n] = -∞

```java

public int findPeakElement(int[] nums) {

? ? ? ? int l = 0, r = nums.length - 1;

? ? ? ? while (l < r) {

? ? ? ? ? ? int mid =? l + (r -l)/2;

? ? ? ? ? ? if (nums[mid] > nums[mid + 1])

? ? ? ? ? ? ? ? r = mid;

? ? ? ? ? ? else

? ? ? ? ? ? ? ? l = mid + 1;

? ? ? ? }

? ? ? ? return l;

? ? }

```

參考：

https://labuladong.gitbook.io/algo/suan-fa-si-wei-xi-lie/er-fen-cha-zhao-xiang-jie

https://blog.csdn.net/bat67/article/details/72049104