用筆一步步演示人工神經(jīng)網(wǎng)絡的反向傳播算法——Jinkey 翻譯

背景

反向傳播訓練（Backpropagation）一個神經(jīng)網(wǎng)絡是一種常見的方法萄金。網(wǎng)上并不缺少介紹反向傳播是如何工作的論文。但很少包括一個用實際數(shù)字的例子。這篇文章是我試圖解釋它是如何工作的和一個具體的例子, 大家可以對比自己的計算,以確保他們正確理解反向傳播噪窘。

Python 實現(xiàn)反向傳播算法

您可以到 Github 嘗試我寫的一個反向傳播算法Python腳本。

反向傳播算法可視化

一個交互式可視化顯示神經(jīng)網(wǎng)絡學習過程, 可以看看我的神經(jīng)網(wǎng)絡可視化網(wǎng)站效扫。

額外的資源

果你發(fā)現(xiàn)本教程有用,想繼續(xù)學習神經(jīng)網(wǎng)絡及其應用,我強烈推薦看看Adrian Rosebrock的優(yōu)秀教程Getting Started with Deep Learning and Python

概述

對于本教程,我們將使用一個有 2 個輸入神經(jīng)元倔监、2 個隱藏的神經(jīng)元和 2 個輸出神經(jīng)元的神經(jīng)網(wǎng)絡直砂。此外,隱藏層和輸出層將包括一個偏差神經(jīng)元（Bias）。
這里的基本結(jié)構(gòu):

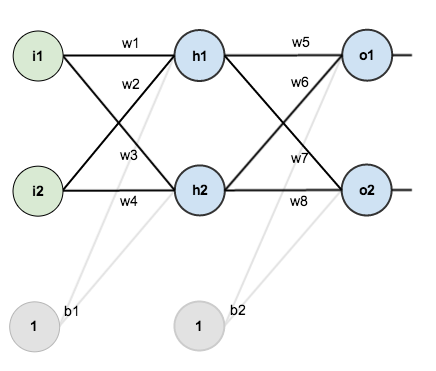
為了一些數(shù)字,這是初始權(quán)重,偏差,和訓練輸入/輸出:

反向傳播的目標是優(yōu)化神經(jīng)網(wǎng)絡的權(quán)重,這樣神經(jīng)網(wǎng)絡可以學習如何正確將任意輸入映射到輸出浩习。
本教程的剩余部分我們要處理一個訓練集:給定輸入0.05和0.10,我們希望神經(jīng)網(wǎng)絡輸出0.01和0.99静暂。

前向傳播

讓我們看看目前神經(jīng)網(wǎng)絡給定的偏差、權(quán)重和輸入的0.05和0.10瘦锹。為此我們要養(yǎng)活這些輸入提前雖然網(wǎng)絡籍嘹。

我們算出每個隱藏神經(jīng)元的總輸入，再利用總輸入作為激活函數(shù)(這里我們使用 Sigmoid 函數(shù))的變量弯院，然后在輸出層神經(jīng)元重復這一步驟。

這是我們?nèi)绾斡嬎?code>h1總輸入:

$net_{h1} = w_1 * i_1 w_2 * i_2 b_1 * 1$

$net_{h1} = 0.15 * 0.05 0.2 * 0.1 0.35 * 1 = 0.3775$

然后使用 Sigmoid 函數(shù)計算h1輸出：

$out_{h1} = \frac{1}{1 e^{-net_{h1}}} = \frac{1}{1 e^{-0.3775}} = 0.593269992$

同理得h2輸出：

$out_{h2} = 0.596884378$

我們對輸出層神經(jīng)元重復這個過程泪掀，使用隱層神經(jīng)元的輸出作為輸入听绳。
這是o1的輸出:

$net_{o1} = w_5 * out_{h1} w_6 * out_{h2} b_2 * 1$

$net_{o1} = 0.4 * 0.593269992 0.45 * 0.596884378 0.6 * 1 = 1.105905967$

$out_{o1} = \frac{1}{1 e^{-net_{o1}}} = \frac{1}{1 e^{-1.105905967}} = 0.75136507$

同理得o2輸出：

$out_{o2} = 0.772928465$

計算總誤差

我們現(xiàn)在可以計算每個輸出神經(jīng)元平方誤差和：

$E_{total} = \sum \frac{1}{2}(target - output)^{2}$

例如,o1預期輸出為 0.01，但實際輸出為0.75136507异赫，因此他的誤差是：

$E_{o1} = \frac{1}{2}(target_{o1} - out_{o1})^{2} = \frac{1}{2}(0.01 - 0.75136507)^{2} = 0.274811083$

重復這個過程得到o2(預期輸出是0.99)的誤差是

$E_{o2} = 0.023560026$

因此椅挣，神經(jīng)網(wǎng)絡的總誤差為

$E_{total} = E_{o1} E_{o2} = 0.274811083 0.023560026 = 0.298371109$

反向傳播過程

反向傳播的目標是更新連接的權(quán)重以使每個神經(jīng)元的實際輸出更加接近預期輸出，從而減少每個神經(jīng)元以及整個網(wǎng)絡的誤差塔拳。

輸出層

考慮一下ω5鼠证，我們希望知道ω5的改變對誤差的影響有大多，稱為

$\frac{\partial E_{total}}{\partial w_{5}}$

（誤差對ω5求偏導數(shù)）
根據(jù)我們所知道的鏈式法則得出：

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

可視化我們所做的事情

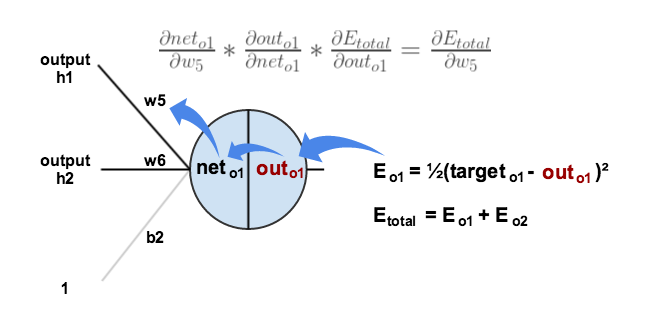
我們需要弄清楚這個等式的每一部分靠抑。
首先量九，o1的輸出變化對總誤差的影響有多大？

$E_{total} = \frac{1}{2}(target_{o1} - out_{o1})^{2} \frac{1}{2}(target_{o2} - out_{o2})^{2}$

$\frac{\partial E_{total}}{\partial out_{o1}} = 2 * \frac{1}{2}(target_{o1} - out_{o1})^{2 - 1} * -1 0$

$\frac{\partial E_{total}}{\partial out_{o1}} = -(target_{o1} - out_{o1}) = -(0.01 - 0.75136507) = 0.74136507$

我們用總誤差對

$out_{o1}$

求偏導數(shù)時颂碧，
$\frac{1}{2}(target_{o2} - out_{o2})^{2}$

的值變?yōu)?0 荠列，因為
$out_{o1}$

不會影響o2的誤差。

下一步载城，o1總輸入的變化對于o1的輸出的影響有多大肌似？

$out_{o1} = \frac{1}{1 e^{-net_{o1}}}$

$\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1 - out_{o1}) = 0.75136507(1 - 0.75136507) = 0.186815602$

最后，計算 ω5的變化對o1總輸入的影響有多大诉瓦？

$net_{o1} = w_5 * out_{h1} w_6 * out_{h2} b_2 * 1$

$\frac{\partial net_{o1}}{\partial w_{5}} = 1 * out_{h1} * w_5^{(1 - 1)} 0 0 = out_{h1} = 0.593269992$

將這三者放在一起：

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

$\frac{\partial E_{total}}{\partial w_{5}} = 0.74136507 * 0.186815602 * 0.593269992 = 0.082167041$

Delta規(guī)則——權(quán)值的修正量等于誤差乘以輸入
我們也可以將這個計算過程組合成 δ規(guī)則的形式：

$\frac{\partial E_{total}}{\partial w_{5}} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1}) * out_{h1}$

（1）

令
$\delta_{o1} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = \frac{\partial E_{total}}{\partial net_{o1}}$

（2）
因為
$net_{o1} = w_5 * out_{h1} w_6 * out_{h2} b_2 * 1$

所以

（3）

聯(lián)立（1）（2）（3）得

$\delta_{o1} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1})$

$\frac{\partial E_{total}}{\partial w_{5}} = \delta_{o1} out_{h1}$

為了減少誤差川队，我們從當前權(quán)重減去這個值（學習率可自定義，這里我們設置為0.5）：

$w_5^{ } = w_5 - \eta * \frac{\partial E_{total}}{\partial w_{5}} = 0.4 - 0.5 * 0.082167041 = 0.35891648$

重復這個過程睬澡，我們可以得到權(quán)重 ω6, ω7, 和 ω8：

$w_6^{ } = 0.408666186$

$w_7^{ } = 0.511301270$

$w_8^{ } = 0.561370121$

我們在得到新的隱藏層神經(jīng)元的輸入權(quán)重之后再更新 ω6, ω7, 和 ω8（也就是說固额，在進行反向傳播的時候我們使用舊的權(quán)重值）

隱藏層

接下來,我們將繼續(xù)向后傳播，計算新值ω1, ω2, ω3, 和 ω4猴贰。
全局來說对雪，我們需要計算

$\frac{\partial E_{total}}{\partial w_{1}} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

可視化：

我們要用類似計算輸出層那樣的過程,但略有不同的是：每個隱層神經(jīng)元的輸出會對多個輸出神經(jīng)元的輸出和誤差產(chǎn)生印象。我們知道out_h1將同時影響out_o1和out_o2（為方便表示米绕，這里用下劃線表示下標瑟捣，下同）馋艺。因此

$\frac{\partial E_{total}}{\partial out_{h1}}$

需要同時考慮out_h1對每個輸出神經(jīng)元的影響：

$\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} \frac{\partial E_{o2}}{\partial out_{h1}}$

先從

$\frac{\partial E_{o1}}{\partial out_{h1}}$

開始：

$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$

我們之前計算過

$\frac{\partial E_{o1}}{\partial net_{o1}}$

：

$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$

然后

$\frac{\partial net_{o1}}{\partial out_{h1}}$

= ω5，因為：

$net_{o1} = w_5 * out_{h1} w_6 * out_{h2} b_2 * 1$

$\frac{\partial net_{o1}}{\partial out_{h1}} = w_5 = 0.40$

講兩者代入

$\frac{\partial E_{o1}}{\partial out_{h1}}$

得：

$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}} = 0.138498562 * 0.40 = 0.055399425$

同理得：

$\frac{\partial E_{o2}}{\partial out_{h1}} = -0.019049119$

因此迈套，

$\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} \frac{\partial E_{o2}}{\partial out_{h1}} = 0.055399425 -0.019049119 = 0.036350306$

現(xiàn)在我們計算好了

$\frac{\partial E_{total}}{\partial out_{h1}}$

捐祠。

然后我們計算

$\frac{\partial out_{h1}}{\partial net_{h1}}$

：

$out_{h1} = \frac{1}{1 e^{-net_{h1}}}$

$\frac{\partial out_{h1}}{\partial net_{h1}} = out_{h1}(1 - out_{h1}) = 0.59326999(1 - 0.59326999 ) = 0.241300709$

接下來我們計算h1的總輸入對ω1求偏導數(shù)：

$net_{h1} = w_1 * i_1 w_2 * i_2 b_1 * 1$

$\frac{\partial net_{h1}}{\partial w_1} = i_1 = 0.05$

綜上所述，

$\frac{\partial E_{total}}{\partial w_{1}} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = 0.036350306 * 0.241300709 * 0.05 = 0.000438568$

你也可以這么寫

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\frac{\partial E_{total}}{\partial out_{o}} * \frac{\partial out_{o}}{\partial net_{o}} * \frac{\partial net_{o}}{\partial out_{h1}}}) * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\delta_{o} * w_{ho}}) * out_{h1}(1 - out_{h1}) * i_{1}$

$\frac{\partial E_{total}}{\partial w_{1}} = \delta_{h1}i_{1}$

現(xiàn)在我們可以更新ω1了：

$w_1^{ } = w_1 - \eta * \frac{\partial E_{total}}{\partial w_{1}} = 0.15 - 0.5 * 0.000438568 = 0.149780716$

重復該過程計算 ω1, ω2, 和 ω3：

$w_2^{ } = 0.19956143$

$w_3^{ } = 0.24975114$

$w_4^{ } = 0.29950229$

最后,我們已經(jīng)更新所有的權(quán)重! 我們最初提出 0.05 和 0.1 的輸入,網(wǎng)絡上的誤差為 0.298371109 桑李。第一輪反向傳播之后,現(xiàn)在總誤差降至 0.291027924 踱蛀。它可能看起來沒有調(diào)整太多。但是在這個過程重復 10000 次之后贵白，比如說率拒，誤差降到0.000035085。在這一時刻禁荒，當我們輸入0.05和0.1時猬膨，兩個輸出神經(jīng)元分別輸出0.015912196 ( vs 預期 0.01) and 0.984065734 (vs 預期 0.99) 。

如果你做到這一步呛伴，發(fā)現(xiàn)任何錯誤或者能想到更通俗易懂的說明方法勃痴，請加我公眾號 jinkey-love 交流。

英文原文鏈接

最后編輯于：2017.12.05 07:34:25

?著作權(quán)歸作者所有,轉(zhuǎn)載或內(nèi)容合作請聯(lián)系作者

人面猴
序言：七十年代末热康，一起剝皮案震驚了整個濱河市沛申，隨后出現(xiàn)的幾起案子，更是在濱河造成了極大的恐慌姐军，老刑警劉巖铁材，帶你破解...
沈念sama閱讀 216,372評論 6贊 498
死咒
序言：濱河連續(xù)發(fā)生了三起死亡事件，死亡現(xiàn)場離奇詭異庶弃，居然都是意外死亡衫贬，警方通過查閱死者的電腦和手機，發(fā)現(xiàn)死者居然都...
沈念sama閱讀 92,368評論 3贊 392
救了他兩次的神仙讓他今天三更去死
文/潘曉璐我一進店門歇攻，熙熙樓的掌柜王于貴愁眉苦臉地迎上來固惯，“玉大人，你說我怎么就攤上這事缴守≡岷粒” “怎么了？”我有些...
開封第一講書人閱讀 162,415評論 0贊 353
道士緝兇錄：失蹤的賣姜人
文/不壞的土叔我叫張陵屡穗，是天一觀的道長贴捡。經(jīng)常有香客問我，道長村砂，這世上最難降的妖魔是什么烂斋？我笑而不...
開封第一講書人閱讀 58,157評論 1贊 292
?港島之戀（遺憾婚禮）
正文為了忘掉前任，我火速辦了婚禮，結(jié)果婚禮上汛骂，老公的妹妹穿的比我還像新娘罕模。我一直安慰自己，他們只是感情好帘瞭，可當我...
茶點故事閱讀 67,171評論 6贊 388
惡毒庶女頂嫁案：這布局不是一般人想出來的
文/花漫我一把揭開白布淑掌。她就那樣靜靜地躺著，像睡著了一般蝶念。火紅的嫁衣襯著肌膚如雪抛腕。梳的紋絲不亂的頭發(fā)上，一...
開封第一講書人閱讀 51,125評論 1贊 297
城市分裂傳說
那天媒殉，我揣著相機與錄音担敌，去河邊找鬼。笑死廷蓉，一個胖子當著我的面吹牛柄错，可吹牛的內(nèi)容都是我干的。我是一名探鬼主播苦酱，決...
沈念sama閱讀 40,028評論 3贊 417
雙鴛鴦連環(huán)套：你想象不到人心有多黑
文/蒼蘭香墨我猛地睜開眼，長吁一口氣：“原來是場噩夢啊……” “哼给猾！你這毒婦竟也來了疫萤？” 一聲冷哼從身側(cè)響起，我...
開封第一講書人閱讀 38,887評論 0贊 274
萬榮殺人案實錄
序言：老撾萬榮一對情侶失蹤敢伸，失蹤者是張志新（化名）和其女友劉穎扯饶，沒想到半個月后，有當?shù)厝嗽跇淞掷锇l(fā)現(xiàn)了一具尸體池颈，經(jīng)...
沈念sama閱讀 45,310評論 1贊 310
?護林員之死
正文獨居荒郊野嶺守林人離奇死亡尾序，尸身上長有42處帶血的膿包…… 初始之章·張勛以下內(nèi)容為張勛視角年9月15日...
茶點故事閱讀 37,533評論 2贊 332
?白月光啟示錄
正文我和宋清朗相戀三年，在試婚紗的時候發(fā)現(xiàn)自己被綠了躯砰。大學時的朋友給我發(fā)了我未婚夫和他白月光在一起吃飯的照片每币。...
茶點故事閱讀 39,690評論 1贊 348
活死人
序言：一個原本活蹦亂跳的男人離奇死亡，死狀恐怖琢歇，靈堂內(nèi)的尸體忽然破棺而出兰怠，到底是詐尸還是另有隱情，我是刑警寧澤李茫，帶...
沈念sama閱讀 35,411評論 5贊 343
?日本核電站爆炸內(nèi)幕
正文年R本政府宣布揭保，位于F島的核電站，受9級特大地震影響魄宏，放射性物質(zhì)發(fā)生泄漏秸侣。R本人自食惡果不足惜，卻給世界環(huán)境...
茶點故事閱讀 41,004評論 3贊 325
男人毒藥：我在死后第九天來索命
文/蒙蒙一、第九天我趴在偏房一處隱蔽的房頂上張望味榛。院中可真熱鬧椭坚，春花似錦、人聲如沸励负。這莊子的主人今日做“春日...
開封第一講書人閱讀 31,659評論 0贊 22
一樁弒父案，背后竟有這般陰謀
文/蒼蘭香墨我抬頭看了看天上的太陽继榆。三九已至巾表，卻和暖如春，著一層夾襖步出監(jiān)牢的瞬間略吨，已是汗流浹背集币。一陣腳步聲響...
開封第一講書人閱讀 32,812評論 1贊 268
情欲美人皮
我被黑心中介騙來泰國打工，沒想到剛下飛機就差點兒被人妖公主榨干…… 1. 我叫王不留翠忠，地道東北人鞠苟。一個月前我還...
沈念sama閱讀 47,693評論 2贊 368
代替公主和親
正文我出身青樓，卻偏偏與公主長得像秽之，于是被迫代替她去往敵國和親当娱。傳聞我的和親對象是個殘疾皇子，可洞房花燭夜當晚...
茶點故事閱讀 44,577評論 2贊 353

用筆一步步演示人工神經(jīng)網(wǎng)絡的反向傳播算法——Jinkey 翻譯

背景

Python 實現(xiàn)反向傳播算法

反向傳播算法可視化

額外的資源

概述

前向傳播

計算總誤差

反向傳播過程

輸出層

隱藏層

推薦閱讀更多精彩內(nèi)容