動(dòng)態(tài)規(guī)劃（Dynamic Programming）

本文包括：

1. 動(dòng)態(tài)規(guī)劃定義
2. 狀態(tài)轉(zhuǎn)移方程
3. 動(dòng)態(tài)規(guī)劃算法步驟
4. 最長(zhǎng)非降子序列（LIS）
5. 最大乘積子串
6. Unique Paths
7. Unique Paths II
8. Minimum Path Sum
9. Triangle
10. 最長(zhǎng)公共自序列（LCS）
11. 編輯距離
12. 交替字符串
13. 矩陣鏈乘積

前文引自：http://www.hawstein.com/posts/dp-novice-to-advanced.html

1拖叙、 什么是動(dòng)態(tài)規(guī)劃宜猜，我們要如何描述它？

• 動(dòng)態(tài)規(guī)劃算法通彻暝伲基于一個(gè)遞推公式及一個(gè)或多個(gè)初始狀態(tài)。 當(dāng)前子問(wèn)題的解將由上一次子問(wèn)題的解推出藻糖。使用動(dòng)態(tài)規(guī)劃來(lái)解題只需要多項(xiàng)式時(shí)間復(fù)雜度返咱， 因此它比回溯法爱致、暴力法等要快許多。

• 首先智嚷，我們要找到某個(gè)狀態(tài)的最優(yōu)解卖丸，然后在它的幫助下，找到下一個(gè)狀態(tài)的最優(yōu)解盏道。

2稍浆、“狀態(tài)”代表什么及如何找到它？

• “狀態(tài)”用來(lái)描述該問(wèn)題的子問(wèn)題的解猜嘱。原文中有兩段作者闡述得不太清楚衅枫，跳過(guò)直接上例子。

• 如果我們有面值為1元朗伶、3元和5元的硬幣若干枚弦撩，如何用最少的硬幣湊夠11元？ (表面上這道題可以用貪心算法论皆，但貪心算法無(wú)法保證可以求出解益楼，比如1元換成2元的時(shí)候)

• 首先我們思考一個(gè)問(wèn)題，如何用最少的硬幣湊夠i元(i<11)点晴？為什么要這么問(wèn)呢感凤？ 兩個(gè)原因：1.當(dāng)我們遇到一個(gè)大問(wèn)題時(shí)，總是習(xí)慣把問(wèn)題的規(guī)模變小觉鼻，這樣便于分析討論俊扭。 2.這個(gè)規(guī)模變小后的問(wèn)題和原來(lái)的問(wèn)題是同質(zhì)的，除了規(guī)模變小坠陈，其它的都是一樣的萨惑， 本質(zhì)上它還是同一個(gè)問(wèn)題(規(guī)模變小后的問(wèn)題其實(shí)是原問(wèn)題的子問(wèn)題)捐康。

• 好了，讓我們從最小的i開(kāi)始吧庸蔼。當(dāng)i=0解总，即我們需要多少個(gè)硬幣來(lái)湊夠0元。 由于1姐仅，3花枫，5都大于0，即沒(méi)有比0小的幣值掏膏，因此湊夠0元我們最少需要0個(gè)硬幣劳翰。 (這個(gè)分析很傻是不是？別著急馒疹，這個(gè)思路有利于我們理清動(dòng)態(tài)規(guī)劃究竟在做些什么佳簸。) 這時(shí)候我們發(fā)現(xiàn)用一個(gè)標(biāo)記來(lái)表示這句“湊夠0元我們最少需要0個(gè)硬幣∮北洌”會(huì)比較方便生均， 如果一直用純文字來(lái)表述，不出一會(huì)兒你就會(huì)覺(jué)得很繞了腥刹。

• 那么马胧， 我們用d(i)=j來(lái)表示湊夠i元最少需要j個(gè)硬幣。于是我們已經(jīng)得到了d(0)=0衔峰， 表示湊夠0元最小需要0個(gè)硬幣佩脊。當(dāng)i=1時(shí)，只有面值為1元的硬幣可用垫卤， 因此我們拿起一個(gè)面值為1的硬幣邻吞，接下來(lái)只需要湊夠0元即可，而這個(gè)是已經(jīng)知道答案的葫男， 即d(0)=0抱冷。所以，d(1)=d(1-1)+1=d(0)+1=0+1=1梢褐。當(dāng)i=2時(shí)旺遮， 仍然只有面值為1的硬幣可用，于是我拿起一個(gè)面值為1的硬幣盈咳， 接下來(lái)我只需要再湊夠2-1=1元即可(記得要用最小的硬幣數(shù)量)耿眉，而這個(gè)答案也已經(jīng)知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2鱼响。

• 一直到這里鸣剪，你都可能會(huì)覺(jué)得，好無(wú)聊， 感覺(jué)像做小學(xué)生的題目似的筐骇。因?yàn)槲覀円恢倍贾荒懿僮髅嬷禐?的硬幣债鸡！耐心點(diǎn)， 讓我們看看i=3時(shí)的情況铛纬。當(dāng)i=3時(shí)厌均，我們能用的硬幣就有兩種了：1元的和3元的( 5元的仍然沒(méi)用，因?yàn)槟阈枰獪惖臄?shù)目是3元告唆！5元太多了親)棺弊。 既然能用的硬幣有兩種，我就有兩種方案擒悬。如果我拿了一個(gè)1元的硬幣模她，我的目標(biāo)就變?yōu)榱耍?湊夠3-1=2元需要的最少硬幣數(shù)量。即d(3)=d(3-1)+1=d(2)+1=2+1=3懂牧。 這個(gè)方案說(shuō)的是缝驳，我拿3個(gè)1元的硬幣；第二種方案是我拿起一個(gè)3元的硬幣归苍， 我的目標(biāo)就變成：湊夠3-3=0元需要的最少硬幣數(shù)量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 這個(gè)方案說(shuō)的是运怖，我拿1個(gè)3元的硬幣拼弃。

• 好了，這兩種方案哪種更優(yōu)呢摇展？ 記得我們可是要用最少的硬幣數(shù)量來(lái)湊夠3元的吻氧。所以， 選擇d(3)=1咏连，怎么來(lái)的呢盯孙？具體是這樣得到的：d(3)=min{d(3-1)+1, d(3-3)+1}。

• 從以上的文字中祟滴， 我們要抽出動(dòng)態(tài)規(guī)劃里非常重要的兩個(gè)概念：狀態(tài)和狀態(tài)轉(zhuǎn)移方程振惰。

• 上文中d(i)表示湊夠i元需要的最少硬幣數(shù)量，我們將它定義為該問(wèn)題的”狀態(tài)”垄懂， 這個(gè)狀態(tài)是怎么找出來(lái)的呢骑晶？我在另一篇文章 動(dòng)態(tài)規(guī)劃之背包問(wèn)題(一)中寫過(guò)： 根據(jù)子問(wèn)題定義狀態(tài)。你找到子問(wèn)題草慧，狀態(tài)也就浮出水面了桶蛔。 最終我們要求解的問(wèn)題，可以用這個(gè)狀態(tài)來(lái)表示：d(11)漫谷，即湊夠11元最少需要多少個(gè)硬幣仔雷。

• 那狀態(tài)轉(zhuǎn)移方程是什么呢？既然我們用d(i)表示狀態(tài)，那么狀態(tài)轉(zhuǎn)移方程自然包含d(i)碟婆， 上文中包含狀態(tài)d(i)的方程是：d(3)=min{d(3-1)+1, d(3-3)+1}电抚。沒(méi)錯(cuò)至耻， 它就是狀態(tài)轉(zhuǎn)移方程协屡，描述狀態(tài)之間是如何轉(zhuǎn)移的。當(dāng)然粘都，我們要對(duì)它抽象一下肘迎，

    d(i)=min{ d(i-vj)+1 }甥温，其中i-vj >=0，vj表示第j個(gè)硬幣的面值;
  

• 偽代碼：

• 依次計(jì)算妓布，可以計(jì)算出11元至少要3枚硬幣姻蚓。

3、DP 算法步驟

• 動(dòng)態(tài)規(guī)劃算法一般用來(lái)求解最優(yōu)化問(wèn)題匣沼，當(dāng)問(wèn)題有很多可行解狰挡，而題目要求尋找這些解當(dāng)中的“最大值”/“最小值”時(shí)，通呈吞危可以采用DP加叁。

• 動(dòng)態(tài)規(guī)劃算法與分治法相似，都是通過(guò)組合子問(wèn)題的解來(lái)求解原問(wèn)題唇撬。所不同的是它匕，動(dòng)態(tài)規(guī)劃應(yīng)用于子問(wèn)題重疊的情況，在遞歸求解子問(wèn)題的時(shí)候窖认，一些子子問(wèn)題可能是相同的豫柬，這種情況下，分治法會(huì)反復(fù)地計(jì)算同樣的子問(wèn)題扑浸，而動(dòng)態(tài)規(guī)劃對(duì)于相同的子問(wèn)題只計(jì)算一次烧给。

• 動(dòng)態(tài)規(guī)劃算法的設(shè)計(jì)步驟：

    1、刻畫最優(yōu)解的結(jié)構(gòu)特征（尋找最優(yōu)子結(jié)構(gòu)）
    2喝噪、遞歸地定義最優(yōu)解的值（確定遞歸公式础嫡，動(dòng)態(tài)規(guī)劃法的重點(diǎn)就是這個(gè)）
    3、計(jì)算最優(yōu)解的值（有兩種方法：帶備忘錄自頂向下法酝惧、自底向上法）
    4驰吓、利用計(jì)算出的信息構(gòu)造一個(gè)最優(yōu)解（通常是將具體的最優(yōu)解輸出）
  

最優(yōu)子結(jié)構(gòu)：?jiǎn)栴}的最優(yōu)解包含的子問(wèn)題的解相對(duì)于子問(wèn)題而言也是最優(yōu)的。
并非所有組合優(yōu)化問(wèn)題都具有最優(yōu)子結(jié)構(gòu)特性系奉。

4檬贰、最長(zhǎng)非降子序列（LIS）

• 問(wèn)題描述：

  一個(gè)序列有N個(gè)數(shù)：A[1],A[2],…,A[N]，求出最長(zhǎng)非降子序列的長(zhǎng)度缺亮。
  (講DP基本都會(huì)講到的一個(gè)問(wèn)題LIS：longest increasing subsequence)

• 思路：

  假如我們考慮求A[1],A[2],…,A[i]的最長(zhǎng)非降子序列的長(zhǎng)度翁涤，其中i<N桥言， 那么上面的問(wèn)題變成了原問(wèn)題的一個(gè)子問(wèn)題(問(wèn)題規(guī)模變小了，你可以讓i=1,2,3等來(lái)分析)

  然后我們定義d(i)葵礼，表示前i個(gè)數(shù)中以A[i]結(jié)尾的最長(zhǎng)非降子序列的長(zhǎng)度号阿。

  如果我們把d(1)到d(N)都計(jì)算出來(lái)，那么最終我們要找的答案就是這里面最大的那個(gè)鸳粉。

  OK扔涧，狀態(tài)找到了，下一步找出狀態(tài)轉(zhuǎn)移方程届谈。

• 可以舉個(gè)例子枯夜，然后求出前面幾項(xiàng)，找出遞推規(guī)律

  d(i)可以用下面的狀態(tài)轉(zhuǎn)移方程得到：

    d(i) = max{1, d(j)+1},其中j<i,A[j]<=A[i]
  

• Python 代碼：

    def LIS(A):
        d = [0 for i in range(len(A))]
        for i in range(len(A)):
            d[i] = 1   # 就算前面所有元素都比當(dāng)前大艰山，那么至少可以包含自身湖雹，所以長(zhǎng)度默認(rèn)值為1
            for j in range(i):
                if A[i] >= A[j] and d[j]+1 > d[i]:
                    d[i] = d[j] + 1
        return max(d)
  
    A = [5, 3, 4, 8, 6, 7]
    print(LIS(A))
  

另一個(gè)解法：利用LCS思想（第9點(diǎn)）

• 構(gòu)造一個(gè)新序列，B曙搬，它是對(duì)A進(jìn)行降序排列而得摔吏。

• 此時(shí)求最長(zhǎng)非增子序列，調(diào)用LCS-LENGTH即可求出A與B的最長(zhǎng)公共子序列纵装，這個(gè)序列就是最后的解征讲。

5、最大乘積子串

• 題目描述：

  給一個(gè)浮點(diǎn)數(shù)序列橡娄，取最大乘積連續(xù)子串的值诗箍，例如 -2.5，4瀑踢，0，3才避，0.5橱夭，8，-1桑逝，則取出的最大乘積連續(xù)子串為3棘劣，0.5，8楞遏。
  也就是說(shuō)茬暇，上述數(shù)組中，3 0.5 8這3個(gè)數(shù)的乘積30.58=12是最大的寡喝，而且是連續(xù)的糙俗。

• 思路：

  因?yàn)橛姓胸?fù)，下次要處理的 a[i] 可能是負(fù)预鬓，所以每次都要存儲(chǔ)最小的子串乘積值巧骚，負(fù)負(fù)得正，得出的結(jié)果有可能還更大。

• 遞推方程：

    maxend = max(max(maxend * a[i], minend * a[i]), a[i]);
    minend = min(min(maxend * a[i], minend * a[i]), a[i]);
  

• Python 代碼：

    def maxProductSubstring(a):
        maxend, minend, maxresult = a[0], a[0], a[0]
        for i in range(1,len(A)):
            maxend = max(max(maxend * a[i], minend * a[i]), a[i])
            minend = min(min(maxend * a[i], minend * a[i]), a[i])
            maxresult = max(maxend, maxresult)
        return maxresult
  
    A = [-2.5, 4, 0, 3, 0.5, 8, -1]
    print(maxProductSubstring(A))
  

6劈彪、Unique Paths

• Leetcode:62. Unique Paths

  A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

  The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

  How many possible unique paths are there?

• Solution：

    class Solution(object):
        def uniquePaths(self, m, n):
            """
            :type m: int
            :type n: int
            :rtype: int
            """
            c = [[0 for i in range(n+1)] for i in range(m+1)]
            for i in range(n+1):
                c[0][i] = 0
            for i in range(m+1):
                c[i][0] = 0
            for i in range(1, m+1):
                for j in range(1, n+1):
                    if i == 1 and j == 1:
                        c[i][j] = 1
                    else:
                        c[i][j] = c[i-1][j] + c[i][j-1]
            return c[i][j]
  
    sol = Solution()
    print(sol.uniquePaths(1, 1))
  

7竣蹦、Unique Paths II

• Leetcode:63. Unique Paths II

  Follow up for "Unique Paths":

  Now consider if some obstacles are added to the grids. How many unique paths would there be?

  An obstacle and empty space is marked as 1 and 0 respectively in the grid.

  For example,
  There is one obstacle in the middle of a 3x3 grid as illustrated below.

  [
  [0,0,0],
  [0,1,0],
  [0,0,0]
  ]

  The total number of unique paths is 2.

  Note: m and n will be at most 100.

• solution:

    class Solution(object):
        def uniquePathsWithObstacles(self, obstacleGrid):
            """
            :type obstacleGrid: List[List[int]]
            :rtype: int
            """
  
            m = len(obstacleGrid)
            n = len(obstacleGrid[0])
            dp = [[0 for i in range(n+1)] for i in range(m+1)]
            dp[1][1] = 1
            for i in range(1, m+1):
                for j in range(1, n+1):
                    if obstacleGrid[i-1][j-1] == 1:
                        dp[i][j] = 0
                    elif i == 1 and j == 1:
                        dp[1][1] = 1
                    else:
                        dp[i][j] = dp[i-1][j] + dp[i][j-1]
  
            return dp[m][n]
  
    sol = Solution
    obstacleGrid = [
        [0, 0, 0],
        [0, 1, 0],
        [0, 0, 0]
    ]
    print(sol.uniquePathsWithObstacles(sol, obstacleGrid))
  

8、Minimum Path Sum

• Leetcode:64. Minimum Path Sum

  Given a m x n grid filled with non-negative numbers,

  find a path from top left to bottom right which minimizes the sum of all numbers along its path.

  Note: You can only move either down or right at any point in time.

• solution:

    class Solution(object):
        def minPathSum(self, grid):
            """
            :type grid: List[List[int]]
            :rtype: int
            """
            m = len(grid)
            if m > 0 and len(grid[0]) > 0:
                n = len(grid[0])
            else:
                return 0
  
            dp = [[0 for i in range(n+1)] for i in range(m+1)]
            for i in range(m+1):
                dp[i][0] = float('inf')
            for i in range(n+1):
                dp[0][i] = float('inf')
            dp[1][1] = grid[0][0]
            for i in range(1, m+1):
                for j in range(1, n+1):
                    if i == 1 and j == 1:
                        dp[i][j] = grid[i-1][j-1]
                    elif dp[i-1][j] < dp[i][j-1]:
                        dp[i][j] = dp[i-1][j] + grid[i-1][j-1]
                    else:
                        dp[i][j] = dp[i][j-1] + grid[i-1][j-1]
            return dp[m][n]
  

9沧奴、Triangle

• Leetcode:120. Triangle

  Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

  For example, given the following triangle

    [
           [2],
          [3,4],
         [6,5,7],
        [4,1,8,3]
    ]
  

  The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

  Note:
  Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

• 第一次嘗試：

    class Solution(object):
        def minimumTotal(self, triangle):
            """
            :type triangle: List[List[int]]
            :rtype: int
            """
            length = len(triangle)
            minSum = triangle[0][0]
            index = 0
            for i in range(1, length):
                if triangle[i][index] < triangle[i][index+1]:
                    minSum += triangle[i][index]
                else:
                    minSum += triangle[i][index+1]
                    index += 1
            return minSum
  

  解釋：
  有點(diǎn)類似于貪心痘括，每一步都尋找最優(yōu)的，但是卻沒(méi)想到滔吠，全局最優(yōu)可能是另外一種情況纲菌，比如下面的測(cè)試用例：

    Submission Result: Wrong Answer More Details 
  
    Input:
    [[-1],[2,3],[1,-1,-3]]
    Output:
    0
    Expected:
    -1
  

  很明顯，按照我的程序屠凶，走法是：-1 2 -1 = 0驰后。
  但是其實(shí)最優(yōu)解是 -1 3 -3 = -1。

• 需要輔助空間 O(n^2) 的 DP 解法：

    '''
        extra space: O(n^2)
        using 'top to bottom' thought
    '''
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        length = len(triangle)
        dp = [[0 for i in range(j+1)] for j in range(length)] # dp[i][j] means element of row i column j is the last one of the min_path
        dp[0][0] = triangle[0][0]
        for i in range(1, length):
            for j in range(i+1):
                if j == 0:
                    dp[i][j] = dp[i-1][j] + triangle[i][j]
                elif j == i:
                    dp[i][j] = dp[i-1][j-1] + triangle[i][j]
                elif dp[i-1][j] < dp[i-1][j-1]:
                    dp[i][j] = dp[i-1][j] + triangle[i][j]
                else:
                    dp[i][j] = dp[i-1][j-1] + triangle[i][j]
        return min(dp[length-1])
  

  理解不難矗愧，同樣是構(gòu)建二維數(shù)組灶芝，dp[i][j] 的意思是以 triangle[i][j] 結(jié)尾的最小路徑和。這其實(shí)就是帶備忘錄的自頂向下辦法唉韭。

• 需要輔助空間 O(n) 的 DP 解法（推薦Ｒ固椤）：

    '''
        extra space: O(n)
        using 'bottom to top' thought
    '''
    def minimumTotal_bottomtotop(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        length = len(triangle)
        dp = triangle[length-1]
        for i in range(length-2, -1, -1):
            for j in range(i+1):
                dp[j] = min(dp[j], dp[j+1]) + triangle[i][j]
        return dp[0]
  

  這種辦法是從底往上，dp 只是一維數(shù)組属愤，在每層操作時(shí)女器，僅記錄該層的各元素結(jié)尾的最小路徑和，并且路徑是從底往上住诸。在處理不同層時(shí)驾胆，dp 根據(jù)下一層的計(jì)算結(jié)果算出當(dāng)前層的值，所以一直在變贱呐。輔助空間只有 O(n)丧诺。

10、最長(zhǎng)公共子序列（LCS）

• 最長(zhǎng)公共子序列（Longest Common Subsequence）是一個(gè)在一個(gè)序列集合中（通常為兩個(gè)序列）用來(lái)查找所有序列中最長(zhǎng)子序列的問(wèn)題奄薇。這與查找最長(zhǎng)公共子串的問(wèn)題不同的地方是：子序列不需要在原序列中占用連續(xù)的位置 驳阎。最長(zhǎng)公共子序列問(wèn)題是一個(gè)經(jīng)典的計(jì)算機(jī)科學(xué)問(wèn)題，也是數(shù)據(jù)比較程序馁蒂，比如Diff工具呵晚，和生物信息學(xué)應(yīng)用的基礎(chǔ)。它也被廣泛地應(yīng)用在版本控制沫屡，比如Git用來(lái)調(diào)和文件之間的改變饵隙。

• LCS 問(wèn)題可以用動(dòng)態(tài)規(guī)劃思想完美解決：

  • 設(shè)二維數(shù)組 f[i][j] 表示：數(shù)組 X 的前 i 位與數(shù)組 Y 的前 j 位的最長(zhǎng)公共子序列的長(zhǎng)度

  • 則有：

    f[i][j] = same(1,1)
    f[i][j] = max{f[i-1][j-1] + same(i,j), f[i-1][j], f[i][j-1]}
    

  • 其中，same(a,b) 表示：當(dāng) X 的第 a 位與 Y的第 b 位完全相同時(shí)為“1”沮脖，否則為“0”癞季。

• 綜上劫瞳，可以總結(jié)出如下的算法，用B[i,j]來(lái)作標(biāo)記绷柒，

    用"↖"表示序列 X 和 Y 的當(dāng)前最后兩項(xiàng) x[i] 和  y[j] 相等志于；
    用“↑”表示選擇時(shí)不考慮 x[i]，即 f[i][j] = f[i-1][j];
    用“←”表示選擇時(shí)不考慮 y[j]废睦，即 f[i][j] = f[i][j-1]
  
    LCS_LENGTH(X, Y):
    for i := 1 to m
        C[i,0] := 0
    for j := 1 to n
        C[0,j] := 0
    for i := 1 to m
        for j := 1 to n
            if X[i] = Y[j]
                C[i,j] := C[i-1,j-1] + 1
                B[i,j] := "↖"
            else if C[i-1,j] >= C[i, j-1]
                C[i,j] := C[i-1,j]
                B[i,j] := "↑"
            else
                C[i,j] := C[i,j-1]
                B[i,j] : "←"
  

• 為了更加直觀伺绽，這里用圖表形象給出：

  

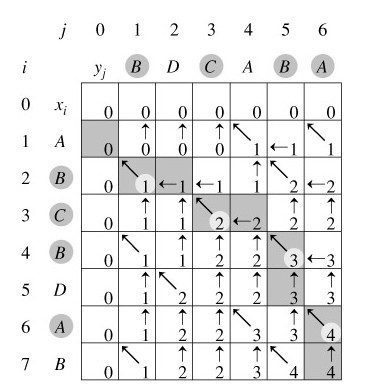
• Python 代碼（A表示↖，T表示↑嗜湃，L表示←）：

    def LCS_LENGTH(X, Y):
        m = len(X)
        n = len(Y)
        c = [[0 for i in range(n+1)] for i in range(m+1)]
        b = [[0 for i in range(n)] for i in range(m)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if X[i-1] == Y[j-1]:
                    c[i][j] = c[i-1][j-1] + 1
                    b[i-1][j-1] = "A"
                elif c[i-1][j] >= c[i][j-1]:
                    c[i][j] = c[i-1][j]
                    b[i-1][j-1] = "T"
                else:
                    c[i][j] = c[i][j-1]
                    b[i-1][j-1] = "L"
        return c, b
  
  
    def print_lcs(b, X, i, j):
        if i == -1 or j == -1:
            return
        if b[i][j] == "A":
            print_lcs(b, X, i-1, j-1)
            print(X[i])
        elif b[i][j] == "T":
            print_lcs(b, X, i-1, j)
        else:
            print_lcs(b, X, i, j-1)
        return
  
    Y = "BDCABA"
    X = "ABCBDAB"
    c, b = LCS_LENGTH(X, Y)
    print_lcs(b, X, len(X)-1, len(Y)-1)
  

• 代碼細(xì)節(jié)：

  • 創(chuàng)建二維數(shù)組奈应，并且不會(huì)出現(xiàn)引用的問(wèn)題（引用問(wèn)題是一改就改了多處）

    c = [[0 for i in range(n+1)] for i in range(m+1)]
    

  • b 是輔助的一個(gè)二維數(shù)組（表），用來(lái)指示當(dāng)前的路徑選擇（走對(duì)角A购披，還是走上T杖挣，還是走左L），實(shí)際上刚陡，《算法導(dǎo)論》中也明確指出這里可以省略惩妇，進(jìn)而在 print_lcs 過(guò)程中做比較，這樣可以節(jié)省輔助空間筐乳，但是這樣比較淺顯易懂

    2017924-LCSb

  • 構(gòu)造完表后歌殃，就可以調(diào)用 print_lcs 過(guò)程來(lái)得到路徑了，在過(guò)程中使用了遞歸的思想蝙云，并且最后輸出的順序是從字符串的左邊到右邊的

    "C:\Program Files\Python36\python.exe" D:/PythonProject/DataStructure-Algorithm/DynamicProgramming/LCS.py
    B
    C
    B
    A
    
    Process finished with exit code 0
    

11氓皱、編輯距離

• 題目描述：

  給定一個(gè)源串和目標(biāo)串，能夠?qū)υ创M(jìn)行如下操作：

  1. 在給定位置上插入一個(gè)字符
  2. 替換任意字符
  3. 刪除任意字符

  寫一個(gè)程序勃刨，返回最小操作數(shù)波材，使得對(duì)源串進(jìn)行這些操作后等于目標(biāo)串，源串和目標(biāo)串的長(zhǎng)度都小于2000身隐。

• 思路：

  動(dòng)態(tài)規(guī)劃廷区，構(gòu)建二維數(shù)組，注意二維數(shù)組的第0行和第0列不是全0的抡医。

  可以想象躲因，如果source 為空早敬，想要轉(zhuǎn)換為 target忌傻，則肯定要執(zhí)行 len(target) = n 次操作，所以dp[i][j]賦初值時(shí)要注意這點(diǎn)搞监。

• 遞推方程：

    //dp[i,j]表示表示源串S[0…i] 和目標(biāo)串T[0…j] 的最短編輯距離
    dp[i,j] = min {dp[i-1,j]+1, dp[i,j-1]+1, dp[i-1,j-1] + (s[i] == t[j] ? 0 : 1) }
    //分別表示：刪除1個(gè)水孩，添加1個(gè)，替換1個(gè)（相同就不用替換）琐驴。
  

• 解釋：

  • 插入是A在和B的前j-1個(gè)比俘种，然后再在A的基礎(chǔ)上進(jìn)行插入一個(gè)字符秤标，插入的字符是B的第j位，所以插入的代價(jià)是dp[i][j-1]+1

  • 刪除是A的前i-1個(gè)和B的j個(gè)比宙刘，因?yàn)榘袮刪除了一個(gè)字符苍姜，所以刪除的代價(jià)是dp[i-1][j]+1

  • 替換是A的前i-1個(gè)和B的j-1個(gè)比，然后把A的第i位變成B的第j位悬包。所以編輯的代價(jià)是dp[i-1][j-1]+1

• python 代碼：

    def editDistance(source, target):
        m = len(source)
        n = len(target)
  
        dp = [[0 for i in range(n+1)] for i in range(m+1)]
        for i in range(n+1):
            dp[0][i] = i
        for i in range(m+1):
            dp[i][0] = i
  
        for i in range(1, m+1):
            for j in range(1, n+1):
                if source[i-1] == target[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(min(dp[i][j-1], dp[i-1][j]), dp[i-1][j-1]) + 1
        return dp[m][n]
  
    source = "abc"
    target = "axxxbxxxc"
    print(editDistance(source, target))
  

12衙猪、交替字符串

• Leetcode: 97. Interleaving String

• 題目描述：

  輸入三個(gè)字符串s1、s2和s3布近，判斷第三個(gè)字符串s3是否由前兩個(gè)字符串s1和s2交錯(cuò)而成垫释，即不改變s1和s2中各個(gè)字符原有的相對(duì)順序，

  例如當(dāng)s1 = “aabcc”撑瞧，s2 = “dbbca”棵譬，s3 = “aadbbcbcac”時(shí)，則輸出true预伺，但如果s3=“accabdbbca”订咸，則輸出false。

• 思路：

  多個(gè)字符串做“比較”的問(wèn)題扭屁，大多都可以用DP求解算谈。

  構(gòu)建二維數(shù)組，一般其規(guī)模為：(m+1)*(n+1)料滥。

  令dp[i][j]代表s3[0...i+j-1]是否由s1[0...i-1]和s2[0...j-1]的字符組成然眼。

  自然，我們的想法是遍歷s3中的每個(gè)元素葵腹，然而要如何找到遞推關(guān)系呢高每？

  因?yàn)橹恍枰敵鰐rue或false，那么我們可以只計(jì)算true的情形践宴，其余情況全是false鲸匿。

  假設(shè)dp[i-1][j]為true，那么dp[i][j]為true的條件就是s1[i-1]是否等于s3[i+j-1]阻肩。
  假設(shè)dp[i][j-1]為true带欢，那么dp[i][j]為true的條件就是s2[j-1]是否等于s3[i+j-1]。

• 由此遞推關(guān)系就可以求出：

    dp[i][j]= (dp[i][j-1]  && str2[j-1]==str3[i+j-1])  || (dp[i-1][j]   && str1[i-1]==str3[i+j-1])
  

• Python 代碼：

    def isInterleave(s1, s2, s3):
        m = len(s1)
        n = len(s2)
        k = len(s3)
        if k != m + n:
            return False
        dp = [[False for i in range(n + 1)] for i in range(m + 1)]
        dp[0][0] = True
        # if s1[0] == s3[0]:
        #     dp[1][0] = True
        # if s2[0] == s3[0]:
        #     dp[0][1] = True
        for i in range(m+1):
            for j in range(n+1):
                if i != 0 or j != 0:
                    if dp[i-1][j] is True and s1[i-1] == s3[i+j-1]:
                        dp[i][j] = True
                    elif dp[i][j-1] is True and s2[j-1] == s3[i+j-1]:
                        dp[i][j] = True
                    else:
                        dp[i][j] = False
        return dp[i][j]
  
    s1 = "xyz"
    s2 = "abc"
    s3 = "xyzabc"
    print(isInterleave(s1, s2, s3))
  

13烤惊、矩陣鏈乘積

• 矩陣鏈乘積（英語(yǔ)：Matrix chain multiplication乔煞，或Matrix Chain Ordering Problem，MOCP）是可用動(dòng)態(tài)規(guī)劃解決的最佳化問(wèn)題柒室。給定一序列矩陣渡贾，期望求出相乘這些矩陣的最有效方法。此問(wèn)題并不是真的去執(zhí)行其乘法雄右，而只是決定執(zhí)行乘法的順序而已空骚。

• 因?yàn)榫仃嚦朔ň哂薪Y(jié)合律纺讲，所有其運(yùn)算順序有很多種選擇。換句話說(shuō)囤屹，不論如何括號(hào)其乘積熬甚，最后結(jié)果都會(huì)是一樣的。例如肋坚，若有四個(gè)矩陣ABCD,將可以有：

    ABCD = (AB)(CD) = A(BC)D = AB(CD) ...
  

• 但括號(hào)其乘積的順序是會(huì)影響到需計(jì)算乘積所需簡(jiǎn)單算術(shù)的數(shù)目则涯，假定各矩陣維數(shù)分別為 10x100 100x5 5x50，如果按 ((AB)C) 的加括號(hào)方式冲簿，要執(zhí)行7500次標(biāo)量乘法粟判，而按(A(BC))的加括號(hào)方式，要執(zhí)行75000次標(biāo)量乘法峦剔。

• 那要如何決定n個(gè)矩陣相乘的最佳順序呢档礁？可以比較每一順序的運(yùn)算量（使用蠻力），但這將需要時(shí)間O(2^n)吝沫，是一種非常慢且對(duì)大n不實(shí)在的方法呻澜。那解決方法，如我們將看到的惨险，是將問(wèn)題分成一套相關(guān)的子問(wèn)題羹幸。以解答子問(wèn)題一次而再使用其解答數(shù)次，即可以徹底地得出其所需時(shí)間辫愉。此一方法稱為動(dòng)態(tài)規(guī)劃栅受。

• 動(dòng)態(tài)規(guī)劃算法步驟：

  • 首先思考：若只有兩個(gè)矩陣相乘，則只會(huì)有一種方法去乘它們恭朗，所有其最小成本為乘積的成本屏镊，那么接下來(lái)可以按照如下方法計(jì)算。
  • 取得矩陣的序列且將其分成兩個(gè)子序列痰腮。
  • 找出乘完每一子序列的最小成本而芥。
  • 將成本加起來(lái)，并加上兩個(gè)結(jié)果矩陣相乘的成本膀值。
  • 在每一矩陣序列可分開(kāi)的位置運(yùn)作棍丐，并取其最小值。

• 總結(jié)成狀態(tài)轉(zhuǎn)移方程即為：

    m[i,j] = 0                             i=j
    m[i,j] = min{m[i,k]+m[k+1,j]+Pi-1PkPj} i<j
  

m[i,j] 為 A1A2...Aj 的最優(yōu)完全加括號(hào)所需的最少標(biāo)量乘法次數(shù)沧踏，對(duì)于整個(gè)問(wèn)題來(lái)說(shuō)歌逢，計(jì)算 A1...n 的最節(jié)省方式的代價(jià)自然應(yīng)為 m[1,n]

Pi-1PkPj 是計(jì)算 Ai...k 和 Ak+1...j 的積所消耗的時(shí)間

• 偽代碼：

    Matrix-Chain-Order(int p[])
    {
        n = p.length - 1;
        for (i = 1; i <= n; i++) 
            m[i,i] = 0;
  
        for (l=2; l<=n; l++) { // l is chain length
            for (i=1; i<=n-l+1; i++) {
                j = i+l-1;
                m[i,j] = MAXINT;
                for (k=i; k<=j-1; k++) {
                    q = m[i,k] + m[k+1,j] + p[i-1]*p[k]*p[j];//Matrix Ai has the dimension  p[i-1] x p[i].
                    if (q < m[i,j]) {
                        m[i,j] = q;
                        s[i,j] = k;
                    }
                }
            }
        }
    }
  

  • 稍加考察，可以知道運(yùn)行時(shí)間為 Θ(n^3)悦冀，輔助空間為 Θ(n^2)

• 上述過(guò)程除了確定最少標(biāo)量乘法數(shù)趋翻，還計(jì)算了用于構(gòu)造最優(yōu)解的表格 s[1..n,1..n] 睛琳。每一項(xiàng)s[i,j]記錄了AiAi+1...Aj的最佳加括號(hào)的在Ak和Ak+1之間分裂的值k盒蟆，于是我們知道最終矩陣積A1..n的最佳計(jì)算是A1..s[1,n] As[1,n]+1..n踏烙。

• 于是可以有打印過(guò)程：

    PRINT-OPTIMAL-PARENS(s,i,j)
    if i = j
        then print "A"i
        else print "("
            PRINT-OPTIMAL-PARENS(s,i,s[i,j])
            PRINT-OPTIMAL-PARENS(s,s[i,j]+1,j)
            print ")"