簡述題目
在一個系統(tǒng)中埃唯,有兩種放射性原子A和B撩匕,原子A會衰變成原子B,而原子B也會衰變成原子A墨叛。嚴(yán)格上來說滑沧,這并不是一個“衰變”循環(huán)。一個更加恰當(dāng)?shù)慕忉寫?yīng)當(dāng)是這個系統(tǒng)在保持能量不變的狀態(tài)下可以在原子A和B中相互轉(zhuǎn)化巍实。而描述這個過程的速率方程是這樣的:
(0.1)
(0.2)
利用這個方程解決這個原子數(shù)分別為NA和NB的系統(tǒng)滓技,同時:
衰變周期
方程的解析
假設(shè)某類原子的衰變方程為:
(1.1)
然后對一段時間內(nèi)的原子數(shù)量做泰勒展開:
=N(0)+\frac{dN}{dt}\cdot\Delta t+\frac{1}{2} \cdot \frac{d^2 N}{dt^2}+...)
只取前兩項,則有:
\approx N(0)+\frac{dN}{dt}\cdot\Delta t .)
對(1.1)方程做近似:
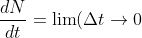\frac{N(t+\Delta t)-N(t)}{t}\approx\frac{N(t+\Delta t)-N(t)}{\Delta t})
所以有:
\approx N(t)+\frac{dN}{dt}\cdot\Delta t.)
由(1.1),有:
\approx N(t)-\frac{N(t)}{t_{dcy}}\cdot\Delta t)
題目方程解析
令:
=N_{B}(t)-N_{A}(t))
由(1.3)知:
\approx N_{A}(0)+\frac{dN_{A}}{dt}\cdot\Delta t)
\approx N_{B}(0)+\frac{dN_{B}}{dt}\cdot\Delta t)
由(1.5)(1.7)知:
\approx N_{A}(t)+\frac{dN_{A}}{dt}\cdot \Delta t \&=N_{A}(t)+\frac{1}{t_{dcy}}\cdot\Delta N(t)\cdot\Delta t\end{align})
\approx N_{B}(t)+\frac{dN_{B}}{dt}\cdot \Delta t \&=N_{B}(t)-\frac{1}{t_{dcy}}\cdot\Delta N(t)\cdot\Delta t\end{align})
代碼模擬
- 我對c語言比較熟悉棚潦,所以先用c語言做模擬令漂,之后再改成python
#include <stdio.h>
#include <math.h>
#define MAX 100
double dt; //time step
double t_decay; //time of decay
double t[MAX];
double N_A[MAX],N_B[MAX]; //number of atoms of A or B
double t_max;
double initialize(double Number_A[],double Number_B[],double time_decay,double dt) //initialize the system
{
printf("initial number of A-atom ->\n");
scanf("%lf",&Number_A[0]);
printf("initila number of B-atom ->\n");
scanf("%lf",&Number_B[0]);
printf("the time of decaying ->");
scanf("%lf",&time_decay);
printf("time step ->");
scanf("%lf",&dt);
t[0]=0.0;
return;
}
double calculate(double Number_A[],double Number_B[],double time_decay,double Delta_N)
{
int i;
for(i=0;i<MAX;i++)
{
Number_A[i+1]=Number_A[i]+((Number_B[i]-Number_A[i])/time_decay)*dt;
Number_B[i+1]=Number_B[i]- ((Number_B[i]-Number_A[i])/time_decay)*dt;
t[i+1]=t[i]+dt;
}
return;
}
double store(double Number_A[],double Number_B[],double t[]) //output the result
{
FILE *fp_out;
int i;
fp_out=fopen("decay_AB.dat","w");
for(i=0;i<MAX;i++)
{
fprintf(fp_out,"%lf\t%lf\t%lf\n",t[i],Number_A[i],Number_B[i]);
}
fclose(fp_out);
return;
}
void main()
{
initialize(N_A,N_B,t_decay,dt);
calculate(N_A,N_B,t_decay,Delta_N);
store(N_A,N_B,t);
}
- python語言部分
import numpy as np
import pylab as pl
Number_A=[]
Number_B=[]
t=[]
print("the number of A atoms ->")
number_a=input()
Number_A.append(number_a)
print("the number of B atoms ->")
number_b=input()
Number_B.append(number_b)
print("the time of decay ->")
t_decay=input()
print("the time step ->")
dt=input()
def Bigger(a,b):
if a>b:
return a
else:
return b
def Smaller(a,b):
if a>b:
return b
else:
return a
big=Bigger(Number_A[0],Number_B[0])
small=Smaller(Number_A[0],Number_B[0])
t.append(0.0)
for i in range(100):
NA=Number_A[i]+((Number_B[i]-Number_A[i])/t_decay)*dt
NB=Number_B[i]+((Number_A[i]-Number_B[i])/t_decay)*dt
tadd=t[i]+dt
Number_A.append(NA)
Number_B.append(NB)
t.append(tadd)
t_max=t[-1]
pl.plot(t,Number_A,'r')
pl.plot(t,Number_B,'g')
pl.title('the decay between A and B')
pl.xlabel('the time of decaying')
pl.ylabel('number of atoms')
pl.xlim(0.0,t_max)
pl.ylim(small,big)
pl.show()
實際模擬(用python做的模擬,比C要方便直觀一些)
模擬1
A原子數(shù)為100,B原子數(shù)為80叠必,衰變周期為1s荚孵,time step為0.05s,模擬結(jié)果為:

A原子數(shù)和B原子數(shù)逐漸趨于一致為90
模擬2
A原子數(shù)為100,B原子數(shù)為0纬朝,衰變周期為1.5s收叶,time step為0.06s,模擬結(jié)果為:

A原子數(shù)與B原子數(shù)依舊趨于一致
結(jié)論
在這樣一個系統(tǒng)中共苛,兩種原子的數(shù)量會逐漸趨于一致判没,且兩種原子數(shù)量的變化率變?yōu)?.實際上是A原子與B原子處于相互轉(zhuǎn)化的動態(tài)平衡中。