紅黑樹

紅黑樹（英語：Red–black tree）是一種自平衡二叉查找樹，典型的用途是實現(xiàn)關(guān)聯(lián)數(shù)組银舱。
它是復(fù)雜的瘪匿，但它的操作有著良好的最壞情況運行時間，并且在實踐中是高效的：它可以在O(log n)時間內(nèi)做查找寻馏，插入和刪除棋弥，這里的n是樹中元素的數(shù)目。

紅黑樹和AVL樹一樣都對插入時間诚欠、刪除時間和查找時間提供了最好可能的最壞情況擔保顽染。這不只是使它們在時間敏感的應(yīng)用如實時應(yīng)用（real time application）中有價值，而且 使它們有在提供最壞情況擔保的其他數(shù)據(jù)結(jié)構(gòu)中作為建造板塊的價值轰绵；例如粉寞，在計算幾何中使用的很多數(shù)據(jù)結(jié)構(gòu)都可以基于紅黑樹。

紅黑樹在函數(shù)式編程中也特別有用左腔，在這里它們是最常用的持久數(shù)據(jù)結(jié)構(gòu)（persistent data structure）之一唧垦，它們用來構(gòu)造關(guān)聯(lián)數(shù)組和集合，每次插入翔悠、刪除之后它們能保持為以前的版本业崖。除了O(log n)的時間之外，紅黑樹的持久版本對每次插入或刪除需要O(log n)的空間蓄愁。

紅黑樹相對于AVL樹來說双炕，犧牲了部分平衡性以換取插入/刪除操作時少量的旋轉(zhuǎn)操作，整體來說性能要優(yōu)于AVL樹撮抓。

紅黑樹性質(zhì)

紅黑樹是每個節(jié)點都帶有顏色屬性的二叉查找樹妇斤，顏色為紅色或黑色。在二叉查找樹強制一般要求以外，對于任何有效的紅黑樹我們增加了如下的額外要求：
1.節(jié)點是紅色或黑色站超。
2.根是黑色荸恕。
3.所有葉子都是黑色（葉子是NIL節(jié)點）。
4.每個紅色節(jié)點必須有兩個黑色的子節(jié)點死相。（從每個葉子到根的所有路徑上不能有兩個連續(xù)的紅色節(jié)點融求。）
5.從任一節(jié)點到其每個葉子的所有簡單路徑都包含相同數(shù)目的黑色節(jié)點。

img

這些約束確保了紅黑樹的關(guān)鍵特性：從根到葉子的最長的可能路徑不多于最短的可能路徑的兩倍長算撮。結(jié)果是這個樹大致上是平衡的生宛。因為操作比如插入、刪除和查找某個值的最壞情況時間都要求與樹的高度成比例肮柜，這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的陷舅，而不同于普通的二叉查找樹。

要知道為什么這些性質(zhì)確保了這個結(jié)果审洞，注意到性質(zhì)4導(dǎo)致了路徑不能有兩個毗連的紅色節(jié)點就足夠了莱睁。最短的可能路徑都是黑色節(jié)點，最長的可能路徑有交替的紅色和黑色節(jié)點芒澜。因為根據(jù)性質(zhì)5所有最長的路徑都有相同數(shù)目的黑色節(jié)點仰剿，這就表明了沒有路徑能多于任何其他路徑的兩倍長。

因為每一個紅黑樹也是一個特化的二叉查找樹撰糠，因此紅黑樹上的只讀操作與普通二叉查找樹上的只讀操作相同酥馍。然而，在紅黑樹上進行插入操作和刪除操作會導(dǎo)致不再匹配紅黑樹的性質(zhì)阅酪≈继唬恢復(fù)紅黑樹的性質(zhì)需要少量（O(logn)）的顏色變更（實際是非常快速的）和不超過三次樹旋轉(zhuǎn)（對于插入操作是兩次）术辐。雖然插入和刪除很復(fù)雜砚尽，但操作時間仍可以保持為O(logn)次。

紅黑樹添加節(jié)點

將一個節(jié)點插入到紅黑樹中辉词，需要執(zhí)行哪些步驟呢必孤？首先，將紅黑樹當作一顆二叉查找樹瑞躺，將節(jié)點插入敷搪；然后，將節(jié)點著色為紅色幢哨；最后赡勘，通過"旋轉(zhuǎn)和重新著色"等一系列操作來修正該樹，使之重新成為一顆紅黑樹捞镰。詳細描述如下：

第一步: 將紅黑樹當作一顆二叉查找樹闸与，將節(jié)點插入毙替。
紅黑樹本身就是一顆二叉查找樹，將節(jié)點插入后践樱，該樹仍然是一顆二叉查找樹厂画。也就意味著，樹的鍵值仍然是有序的拷邢。此外袱院，無論是左旋還是右旋，若旋轉(zhuǎn)之前這棵樹是二叉查找樹瞭稼，旋轉(zhuǎn)之后它一定還是二叉查找樹坑填。這也就意味著，任何的旋轉(zhuǎn)和重新著色操作弛姜，都不會改變它仍然是一顆二叉查找樹的事實。
好吧妖枚？那接下來廷臼，我們就來想方設(shè)法的旋轉(zhuǎn)以及重新著色，使這顆樹重新成為紅黑樹绝页！

第二步：將插入的節(jié)點著色為"紅色"荠商。
為什么著色成紅色，而不是黑色呢续誉？
(1) 每個節(jié)點或者是黑色莱没，或者是紅色。
(2) 根節(jié)點是黑色酷鸦。
(3) 每個葉子節(jié)點是黑色饰躲。 （注意：這里葉子節(jié)點，是指為空的葉子節(jié)點＞矢簟）
(4) 如果一個節(jié)點是紅色的嘹裂，則它的子節(jié)點必須是黑色的。
(5) 從一個節(jié)點到該節(jié)點的子孫節(jié)點的所有路徑上包含相同數(shù)目的黑節(jié)點摔握。

將插入的節(jié)點著色為紅色寄狼，不會違背"特性(5)"！少違背一條特性氨淌，就意味著我們需要處理的情況越少泊愧。

第三步: 通過一系列的旋轉(zhuǎn)或著色等操作，使之重新成為一顆紅黑樹盛正。
第二步中删咱，將插入節(jié)點著色為"紅色"之后，不會違背"特性(5)"蛮艰。那它到底會違背哪些特性呢腋腮？
對于"特性(1)"雀彼，顯然不會違背了。因為我們已經(jīng)將它涂成紅色了即寡。
對于"特性(2)"徊哑，顯然也不會違背。在第一步中聪富，我們是將紅黑樹當作二叉查找樹莺丑，然后執(zhí)行的插入操作。而根據(jù)二叉查找數(shù)的特點墩蔓，插入操作不會改變根節(jié)點梢莽。所以，根節(jié)點仍然是黑色奸披。
對于"特性(3)"昏名，顯然不會違背了。這里的葉子節(jié)點是指的空葉子節(jié)點阵面，插入非空節(jié)點并不會對它們造成影響轻局。
對于"特性(4)"，是有可能違背的样刷！

情形1:新節(jié)點N位于樹的根上仑扑，沒有父節(jié)點。在這種情形下置鼻，我們把它重繪為黑色以滿足性質(zhì)2镇饮。因為它在每個路徑上對黑節(jié)點數(shù)目增加一，性質(zhì)5匹配箕母。

情形2:新節(jié)點的父節(jié)點P是黑色储藐，所以性質(zhì)4沒有失效（新節(jié)點是紅色的）。在這種情形下司蔬，樹仍是有效的邑茄。性質(zhì)5也未受到威脅，盡管新節(jié)點N有兩個黑色葉子子節(jié)點俊啼；但由于新節(jié)點N是紅色肺缕，通過它的每個子節(jié)點的路徑就都有同通過它所替換的黑色的葉子的路徑同樣數(shù)目的黑色節(jié)點，所以依然滿足這個性質(zhì)授帕。

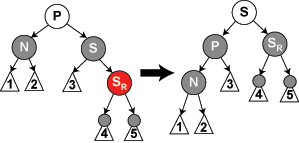
情形3:如果父節(jié)點P和叔父節(jié)點U二者都是紅色同木，（此時新插入節(jié)點N做為P的左子節(jié)點或右子節(jié)點都屬于情形3，這里右圖僅顯示N做為P左子的情形）則我們可以將它們兩個重繪為黑色并重繪祖父節(jié)點G為紅色（用來保持性質(zhì)5）□耸現(xiàn)在我們的新節(jié)點N有了一個黑色的父節(jié)點P彤路。因為通過父節(jié)點P或叔父節(jié)點U的任何路徑都必定通過祖父節(jié)點G，在這些路徑上的黑節(jié)點數(shù)目沒有改變芥映。但是洲尊，紅色的祖父節(jié)點G可能是根節(jié)點远豺，這就違反了性質(zhì)2，也有可能祖父節(jié)點G的父節(jié)點是紅色的坞嘀，這就違反了性質(zhì)4躯护。為了解決這個問題，我們在祖父節(jié)點G上遞歸地進行情形1的整個過程丽涩。（把G當成是新加入的節(jié)點進行各種情形的檢查）

img

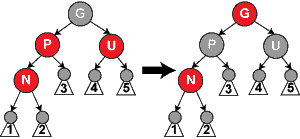
情形4:父節(jié)點P是紅色而叔父節(jié)點U是黑色或缺少棺滞，并且新節(jié)點N是其父節(jié)點P的右子節(jié)點而父節(jié)點P又是其父節(jié)點的左子節(jié)點。在這種情形下矢渊，我們進行一次左旋轉(zhuǎn)調(diào)換新節(jié)點和其父節(jié)點的角色;接著继准，我們按情形5處理以前的父節(jié)點P以解決仍然失效的性質(zhì)4。注意這個改變會導(dǎo)致某些路徑通過它們以前不通過的新節(jié)點N（比如圖中1號葉子節(jié)點）或不通過節(jié)點P（比如圖中3號葉子節(jié)點）矮男，但由于這兩個節(jié)點都是紅色的移必，所以性質(zhì)5仍有效。

img

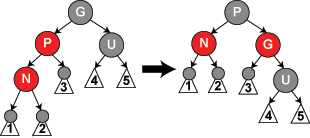
情形5：父節(jié)點P是紅色而叔父節(jié)點U是黑色或缺少毡鉴，新節(jié)點N是其父節(jié)點的左子節(jié)點避凝，而父節(jié)點P又是其父節(jié)點G的左子節(jié)點。在這種情形下眨补，我們進行針對祖父節(jié)點G的一次右旋轉(zhuǎn)；在旋轉(zhuǎn)產(chǎn)生的樹中倒脓，以前的父節(jié)點P現(xiàn)在是新節(jié)點N和以前的祖父節(jié)點G的父節(jié)點撑螺。我們知道以前的祖父節(jié)點G是黑色，否則父節(jié)點P就不可能是紅色（如果P和G都是紅色就違反了性質(zhì)4崎弃，所以G必須是黑色）甘晤。我們切換以前的父節(jié)點P和祖父節(jié)點G的顏色，結(jié)果的樹滿足性質(zhì)4饲做。性質(zhì)5也仍然保持滿足线婚，因為通過這三個節(jié)點中任何一個的所有路徑以前都通過祖父節(jié)點G，現(xiàn)在它們都通過以前的父節(jié)點P盆均。在各自的情形下塞弊，這都是三個節(jié)點中唯一的黑色節(jié)點。

img

紅黑樹刪除節(jié)點

情形1: N是新的根泪姨。在這種情形下游沿，我們就做完了。我們從所有路徑去除了一個黑色節(jié)點肮砾，而新根是黑色的诀黍，所以性質(zhì)都保持著。

情形2： S是紅色仗处。在這種情形下我們在N的父親上做左旋轉(zhuǎn)眯勾，把紅色兄弟轉(zhuǎn)換成N的祖父枣宫，我們接著對調(diào)N的父親和祖父的顏色。完成這兩個操作后吃环，盡管所有路徑上黑色節(jié)點的數(shù)目沒有改變也颤，但現(xiàn)在N有了一個黑色的兄弟和一個紅色的父親（它的新兄弟是黑色因為它是紅色S的一個兒子），所以我們可以接下去按情形4模叙、情形5或情形6來處理歇拆。

img

情形3： N的父親、S和S的兒子都是黑色的范咨。在這種情形下故觅，我們簡單的重繪S為紅色。結(jié)果是通過S的所有路徑渠啊，它們就是以前不通過N的那些路徑输吏，都少了一個黑色節(jié)點。因為刪除N的初始的父親使通過N的所有路徑少了一個黑色節(jié)點替蛉，這使事情都平衡了起來贯溅。但是，通過P的所有路徑現(xiàn)在比不通過P的路徑少了一個黑色節(jié)點躲查，所以仍然違反性質(zhì)5它浅。要修正這個問題，我們要從情形1開始镣煮，在P上做重新平衡處理姐霍。

img

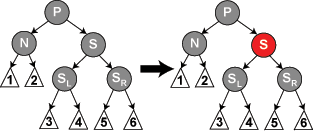
情形4： S和S的兒子都是黑色，但是N的父親是紅色典唇。在這種情形下镊折，我們簡單的交換N的兄弟和父親的顏色。這不影響不通過N的路徑的黑色節(jié)點的數(shù)目介衔，但是它在通過N的路徑上對黑色節(jié)點數(shù)目增加了一恨胚，添補了在這些路徑上刪除的黑色節(jié)點。

img

情形5： S是黑色炎咖，S的左兒子是紅色赃泡，S的右兒子是黑色，而N是它父親的左兒子乘盼。在這種情形下我們在S上做右旋轉(zhuǎn)急迂，這樣S的左兒子成為S的父親和N的新兄弟。我們接著交換S和它的新父親的顏色蹦肴。所有路徑仍有同樣數(shù)目的黑色節(jié)點僚碎，但是現(xiàn)在N有了一個黑色兄弟，他的右兒子是紅色的阴幌，所以我們進入了情形6勺阐。N和它的父親都不受這個變換的影響卷中。

img

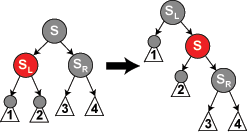
情形6： S是黑色，S的右兒子是紅色渊抽，而N是它父親的左兒子蟆豫。在這種情形下我們在N的父親上做左旋轉(zhuǎn)，這樣S成為N的父親（P）和S的右兒子的父親懒闷。我們接著交換N的父親和S的顏色十减，并使S的右兒子為黑色。子樹在它的根上的仍是同樣的顏色愤估，所以性質(zhì)3沒有被違反帮辟。但是，N現(xiàn)在增加了一個黑色祖先：要么N的父親變成黑色玩焰，要么它是黑色而S被增加為一個黑色祖父由驹。所以，通過N的路徑都增加了一個黑色節(jié)點昔园。
此時蔓榄，如果一個路徑不通過N，則有兩種可能性：

它通過N的新兄弟默刚。那么它以前和現(xiàn)在都必定通過S和N的父親甥郑，而它們只是交換了顏色。所以路徑保持了同樣數(shù)目的黑色節(jié)點荤西。

它通過N的新叔父壹若，S的右兒子。那么它以前通過S皂冰、S的父親和S的右兒子，但是現(xiàn)在只通過S养篓，它被假定為它以前的父親的顏色秃流，和S的右兒子，它被從紅色改變?yōu)楹谏：铣尚Ч沁@個路徑通過了同樣數(shù)目的黑色節(jié)點舶胀。

在任何情況下，在這些路徑上的黑色節(jié)點數(shù)目都沒有改變碧注。所以我們恢復(fù)了性質(zhì)4嚣伐。在示意圖中的白色節(jié)點可以是紅色或黑色，但是在變換前后都必須指定相同的顏色萍丐。

img

--

紅黑樹本身也是一種近似2-3-4樹的數(shù)據(jù)結(jié)構(gòu)轩端。
通常2-3-4樹實現(xiàn)較紅黑樹而言相對復(fù)雜。

img

具體實現(xiàn)：
https://github.com/imstayreal/data-struct-study/tree/master/DataStruct/src/redblack