這是系列教程的第二篇文章棺蛛，公式的推導(dǎo)可能會愈加復(fù)雜炉菲，請認(rèn)真分析并炮！come on~

<h4>符號及標(biāo)記</h4>

在進(jìn)行數(shù)學(xué)運算之前，我們需要規(guī)定一些數(shù)學(xué)標(biāo)記蹋绽，方便接下來的討論:

<h4>函數(shù)向量化</h4>
假設(shè)函數(shù)的向量化
如果我們的假設(shè)函數(shù)是：
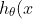=\theta_0 +\theta_1 x_1+\theta_2 x_2 +...+\theta_n x_n)

那么我們可以將上述式子向量化為：
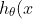=[\theta_0\ \theta_1\ \theta_2\ ...\theta_n]\cdot \begin{bmatrix}1 \ x_1 \ x_2 \ . \ . \ . \ x_n \end{bmatrix}= \theta^T\cdot X)
為了方便計算我們令：

舉個例子卸耘，假設(shè)我們有這樣一個訓(xùn)練集退敦，每個訓(xùn)練樣本的輸入值都橫向展開，如下所示：
} & x_1^{(1)} \ x_0^{(2)} & x_1^{(2)} \ x_0^{(3)} & x_1^{(3)} \end{bmatrix})
比如蚣抗，第一個訓(xùn)練樣本的數(shù)據(jù)集為

其次侈百，參數(shù)的矩陣為：

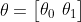
所以有：
 = X\cdot \theta)

代價函數(shù)的向量化
=\frac{1}{2m}\sum_{i=1}^{m}[h_{\theta}\left( x^i \right)-y^{(i)}]2=\frac{1}{2m}(X\theta - \vec{y})^T(X\theta - \vec{y}))

梯度下降算法的公式為：
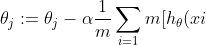-y^{(i)}]x{(i)}_{j})
其中 j=0,1,2, ... , m

將上述公式向量化瓮下，得到：

)
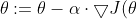=\begin{bmatrix} \frac{\partial}{\partial \theta_0}J(\theta) \ \frac{\partial}{\partial \theta_1}J(\theta) \ \frac{\partial}{\partial \theta_2}J(\theta) \ . \ . \ . \ \frac{\partial}{\partial \theta_m}J(\theta) \end{bmatrix})
其中：
=\frac{1}{m}\sum_{i=1}^{m}x_j{(i)}[h_{\theta}(x^{i})-y{(i)}])
通過分析角標(biāo)之間的關(guān)系，我們可以將上述式子向量化為：
=\frac{1}{m}X^T[X \theta-\vec{y}\ ])

也就是說钝域，我們的梯度下降算法表示為：

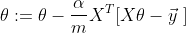
<h4>正規(guī)化方程</h4>
在對訓(xùn)練集應(yīng)用梯度下降算法時讽坏，如果訓(xùn)練集的數(shù)據(jù)比較大，比如上千上萬時例证，我們可能需要花費很長的時間來對訓(xùn)練集進(jìn)行梯度下降路呜，因此，在應(yīng)用訓(xùn)練集數(shù)據(jù)進(jìn)行訓(xùn)練前织咧，我們需要對數(shù)據(jù)做一些預(yù)處理胀葱。

當(dāng)數(shù)據(jù)值比較大的時候，我們可以對數(shù)據(jù)值這樣處理：
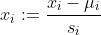
其中u_i是該數(shù)據(jù)樣本的平均值笙蒙，s_i是數(shù)據(jù)樣本的極差（極差的概念請自行百度）抵屿。

當(dāng)然我們也可以有自己的方法對數(shù)據(jù)進(jìn)行處理，只要能方便我們對訓(xùn)練集應(yīng)用梯度下降算法捅位。不過在這里轧葛，我想要介紹利用正規(guī)化方程的方法來直接獲得假設(shè)函數(shù)的參數(shù)值。

如果對于數(shù)據(jù)集X和y艇搀，存在參數(shù)集θ滿足：
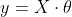
因此有：
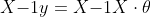
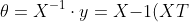^{-1}\cdot X^Ty = (X^T X)^{-1}XT y)

<h4>總結(jié)</h4>

下一篇教程就是實例代碼的實戰(zhàn)尿扯，上面的公式推導(dǎo)請好好消化，當(dāng)然更多內(nèi)容請參考機(jī)器學(xué)習(xí)中符。