CS229學(xué)習(xí)筆記（5）

CS229_5-局部加權(quán)線性回歸

局部加權(quán)線性回歸

欠擬合與過擬合

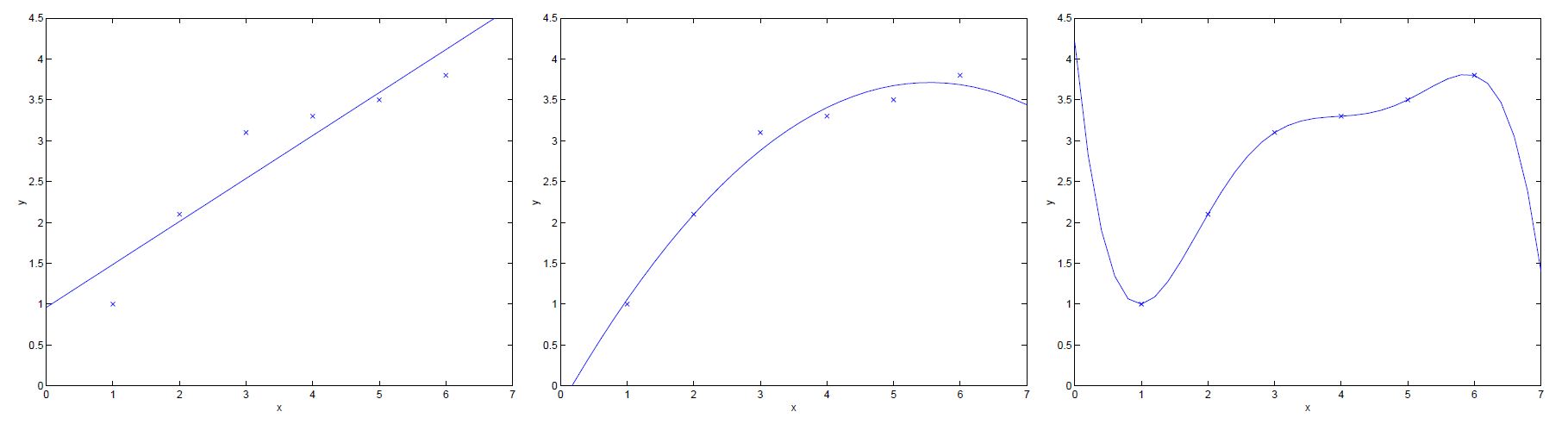
上述三幅圖展示了规丽，不同假設(shè)函數(shù) $h_\theta(x)$ 對于同一訓(xùn)練集的擬合情況傲须。

左圖：假設(shè)函數(shù) $h_\theta(x)$ 為 $h_\theta(x) = \theta_0 + \theta_1x$ 甸鸟。很明顯可看出惦费，其擬合情況不太理想，我們將這種情況稱為欠擬合（under-fitting）抢韭；
右圖：假設(shè)函數(shù) $h_\theta(x)$ 為 $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2$ 薪贫。很明顯可看出，其擬合情況太好了刻恭，以至于其可能對于一些訓(xùn)練集外的數(shù)據(jù)點(diǎn)無法做到很好地預(yù)測瞧省，因此我們將這種情況稱為過擬合（over-fitting）。

因此，我們在設(shè)計假設(shè)函數(shù) $h_\theta(x)$ 時鞍匾，不能過分地追求對訓(xùn)練集的擬合程度勉抓，只需其擬合程度達(dá)到上述圖中中間圖的擬合程度即可。

補(bǔ)充：給定一個假設(shè)空間 $H$ 候学，一個假設(shè) $h$ 屬于 $H$ 藕筋，如果存在其他的假設(shè) $h_1$ ，使得在訓(xùn)練樣例上 $h$ 的錯誤率比 $h_1$ 好梳码，但在整個個實(shí)例分布上 $h_1$ 的錯誤率比 $h$ 小隐圾，那么就說假設(shè) $h$ 出現(xiàn)過擬合的情況。欠擬合的定義與之相似掰茶。^[1]

局部加權(quán)線性回歸算法

局部加權(quán)線性回歸（Locally Weight Linear Regression暇藏，LWR）算法顧名思義為線性回歸算法的擴(kuò)展，當(dāng)目標(biāo)假設(shè)為線性模型時濒蒋，因此我們采用線性回歸盐碱；但如果目標(biāo)假設(shè)不是線性模型，比如一個忽上忽下的的函數(shù)沪伙，這時用線性模型就擬合的很差瓮顽。為了解決這個問題，當(dāng)我們在預(yù)測一個點(diǎn)的值時围橡，我們選擇和這個點(diǎn)相近的點(diǎn)而不是全部的點(diǎn)做線性回歸暖混。基于這個思想翁授，就有了局部加權(quán)回歸算法拣播。

原始線性回歸算法：

找到參數(shù) $\theta$ 使其最小化 $\sum_i(y^{(i)} - \theta^Tx^{(i)})^2$ ；
輸出 $\theta^Tx$ 收擦。

局部加權(quán)線性回歸算法：

找到參數(shù) $\theta$ 使其最小化 $\sum_i \omega^{(i)}(y^{(i)} - \theta^Tx^{(i)})^2$ 贮配；
輸出 $\theta^Tx$ 。

兩者相互比較可知塞赂，在最小化 $\sum_i(y^{(i)} - \theta^Tx^{(i)})^2$ 時泪勒，局部加權(quán)線性回歸算法添加了權(quán)值 $\omega^{(i)}$ 。其作用為根據(jù)要預(yù)測的點(diǎn)與數(shù)據(jù)集中的點(diǎn)的距離來為訓(xùn)練集中的點(diǎn)賦予權(quán)值减途，當(dāng)某點(diǎn)距離待預(yù)測點(diǎn)較遠(yuǎn)時酣藻，其權(quán)重較小鳍置；反之則權(quán)重較大辽剧。

$\omega^{(i)} = exp(-\frac{(x^{(i)} - x)^2}{2\tau^2})$

其中，參數(shù) $\tau$ 稱為波長參數(shù)税产，其控制權(quán)值隨距離增大而下降的速率怕轿。

注：若 $x$ 為向量偷崩，則權(quán)值 $\omega^{(i)}$ 將改寫為：

$\omega^{(i)} = exp(-\frac{(x^{(i)} - x)^T(x^{(i)} - x)}{2\tau^2})$

或者為：

$\omega^{(i)} = exp(-\frac{(x^{(i)} - x)^T\Sigma^{-1}(x^{(i)} - x)}{2})$

補(bǔ)充：

參數(shù)學(xué)習(xí)算法（Parametric Learning Algorithm）是一類有固定數(shù)目參數(shù)的用來進(jìn)行數(shù)據(jù)擬合的算法，線性回歸算法即為此類撞羽；
非參數(shù)學(xué)習(xí)算法（Non-Parametric Learning Algorithm）是一類參數(shù)數(shù)量隨訓(xùn)練集增大而增加的算法阐斜，局部加權(quán)線性回歸算法即為此類。

http://blog.csdn.net/stdcoutzyx/article/details/9113681 ?

最后編輯于：2018.11.10 23:18:11

?著作權(quán)歸作者所有,轉(zhuǎn)載或內(nèi)容合作請聯(lián)系作者