本文來自麻省理工ECE教授Scott Aaronson的教學講義朗若。和我們大多數(shù)人學的物理課不同昌罩,這門課是量子計算,從另外一個角度來理解量子力學遣总。當時讀到這篇文章覺得很有意思,便打算翻譯過來和大家一起分享旭斥。由于本人學識淺薄垂券,翻譯中若有錯誤歡迎大家指正。另外這是課堂講義菇爪,口語化的文字很難翻譯,一些我覺得不重要的內(nèi)容就略去不翻或者意譯了熙揍。
量子力學的教學氏涩,有兩種方法。第一種方法是如今大多數(shù)物理學家采用的是尖,以歷史發(fā)展的順序饺汹,先從經(jīng)典力學講到電動力學,解一大堆微分方程首繁,然后告訴你黑體輻射悖論和那些奇奇怪怪的實驗結(jié)果,這些導致了物理學的危機夹攒。然后你會學習那些物理學家在1900和1926年之間提出來的各種復雜想法來解救這個危機胁塞。幸運的話,經(jīng)過多年的學習你最終接觸到這個中心概念:世界不是由概率(probabilities)描述的编检,而是由一些叫做振幅(amplitudes)的數(shù)字描述的扰才。概率是非負的,而振幅可正可負衩匣,甚至可以是復數(shù)粥航。
如今是量子信息時代生百,所有物理學家都用這種方法來學習量子力學的話就有點可笑。那些受過高等教育的人只不過記住了這些話:“光具有波粒二象性”缀程,“薛定諤的貓不知是死是活除非你打開箱子瞧一瞧”市俊,“你可以知道位置(position)或動量(momentum),但是不能兩個都知道”蠢甲,“一個粒子知道另一個粒子的自旋即使距離很遠” 等等据忘。但是我們根本不能理解這些,除非我們痛苦地學習好多年勇吊。
第二種教學方法拋棄了量子力學的歷史發(fā)展過程汉规,直接跳到其核心概念,也就是一個允許負號的概率理論针史。一旦你理解了這個理論,你就能品嘗物理婚陪,就能計算任意原子的譜帶频祝。這個第二種方法就是我所采用的。
那么什么是量子力學沽一?盡管是由物理學家發(fā)現(xiàn)的漓糙,量子力學和電磁學及廣義相對論相比,并不是同一類的物理學。從科學的繼承性來看拙友,生物學來自化學歼郭,化學來自物理辐棒,物理來自數(shù)學,而量子力學位于物理和數(shù)學之間泰涂。量子力學就像是個操作系統(tǒng)辐怕,而其他物理理論就像是計算機應(yīng)用程序(除了廣義相對論沒能兼容這個系統(tǒng))。甚至可以用一個詞來形容把一個物理理論安裝到這個操作系統(tǒng)上:“量子化”是牢。
如果量子力學不是關(guān)于一般的物理概念(物質(zhì)陕截,能量,波农曲,粒子),那么它是關(guān)于什么的形葬?在我看來暮的,量子力學是關(guān)于信息,概率源织,觀察 以及它們之間的聯(lián)系的理論微猖。
我的觀點是,如果你研究概率論凛剥,那么最后肯定會觸及量子力學。所以我們不如把概率這個概念擴大化逻炊,讓概率也可以取負數(shù)。如果早這么做的話豹休,19世紀的數(shù)學家就可以發(fā)明量子力學了桨吊,根本就不需要實驗。
Scott: 在我看來洛搀,這說明了實驗的重要性佑淀。很多時候我們做實驗是因為我們不夠聰明,必須通過分析實驗結(jié)果來提出理論伸刃。
在這節(jié)課上奕枝,我將不做任何實驗,來向你展示為什么當你希望這個宇宙有普遍的屬性時隘道,你必須從這三個中選:(1)確定性谭梗,(2)經(jīng)典概率論,(3)量子力學激捏。
小于0%的機率
什么是擁有負數(shù)概念的“概率論”? 我們從來沒有聽說過天氣預(yù)報說明天有-20%的可能性下雨闰蛔,這是有悖常理的图柏。先不管這些,讓我們抽象地想想一個事件例诀,擁有N個可能的結(jié)果。我們可以將這個事件用一個向量來表示繁涂。這個向量由N個實數(shù)構(gòu)成:
(P1,...., Pn)
數(shù)學上我們會如何描述這個向量扔罪? 我們會說,這些概率應(yīng)該是非負的步势,而且它們加起來等于1坏瘩。后一條我們可以這樣表示:概率向量的 1-norm 必須是1漠魏。(1-norm 指的是每個元的絕對值加和。)
但是 1-norm 并不是這個世界上唯一的 norm 柱锹,它并不是定義向量“大小”的唯一方式。還有另外的方式來定義壤巷,比如說 2-norm瞧毙, 又叫 Euclidean norm (歐幾里德范數(shù))。歐幾里德范數(shù)指的是向量元平方和的開平方值矩动。
如何概率論是基于 2-norm 而不是 1-norm释漆,那么量子力學就是其結(jié)果。
讓我們來考慮一個比特示姿。在概率論里逊笆,我們描述一個比特是 0 的可能性是 p,那么是 1 的可能性就是 1-p 荧琼。如果我們把 1-norm 變?yōu)?2-norm, 那么就不需要要求這兩個數(shù)字加起來是1命锄,而是要求它們的平方和是1脐恩。(假設(shè)這里討論的數(shù)字還是實數(shù)。)換句話說驶冒,我們需要的是這樣一個向量 (α,β)骗污, 滿足 α^2 + β^2 = 1 (有誰知道m(xù)arkdown如何插入公式?)需忿。 這樣的向量組會形成一個圓:
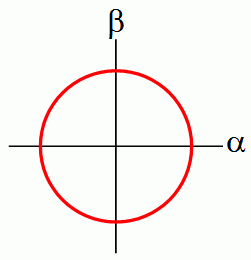
我們的理論必須的和觀察有關(guān), 假設(shè)有一個比特可以用這個向量(α,β)來描述屋厘,那么我們得說明當我們?nèi)?em>看這個比特的時候會發(fā)生什么。既然它是一個比特汗洒,我們應(yīng)該看到0或者1溢谤!而且看到0的幾率和看到1的幾率加起來應(yīng)該是1。那么對于這個(α,β)向量溯香,我們該如何得到兩個加起來等于1的數(shù)字玫坛?很簡單,我們可以讓 α^2 作為結(jié)果是0的概率炕吸,讓 β^2 作為結(jié)果是1的概率勉痴。
那么在這個情況下,我們可以不拋棄 α 和 β蒸矛,直接用概率來描述這個比特?啊....關(guān)鍵的差別在于當我們把一個算子作用在向量上面時向量的變化(這個過程稱為operation)斩祭。在概率論里,如果一個比特用向量(p,1-p)來表示耳奕,那么我們可以用一個隨機矩陣(stochastic matrix)來表示任何對于向量的操作(operation)诬像。
隨機矩陣:一個矩陣由非負實數(shù)構(gòu)成坏挠,每一列加起來和為1。
比如說癞揉,一個 “翻轉(zhuǎn)比特”操作溺欧,把結(jié)果為1的概率從p變成了1-p,那么這個操作可以表示為:
(此處應(yīng)有圖)
未完待續(xù) 歡迎關(guān)注這篇文章芥牌,我會隨時更新的聂使。
2014年12月14日:
這文章爛尾了柏靶,未來某日也許會更新。