2.2 監(jiān)督學(xué)習(xí) II

原文：Machine Learning for Humans, Part 2.1: Supervised Learning

作者：Vishal Maini

譯者：飛龍

協(xié)議：CC BY-NC-SA 4.0

使用對(duì)數(shù)幾率回歸（LR）和支持向量機(jī)（SVM）的分類壁公。

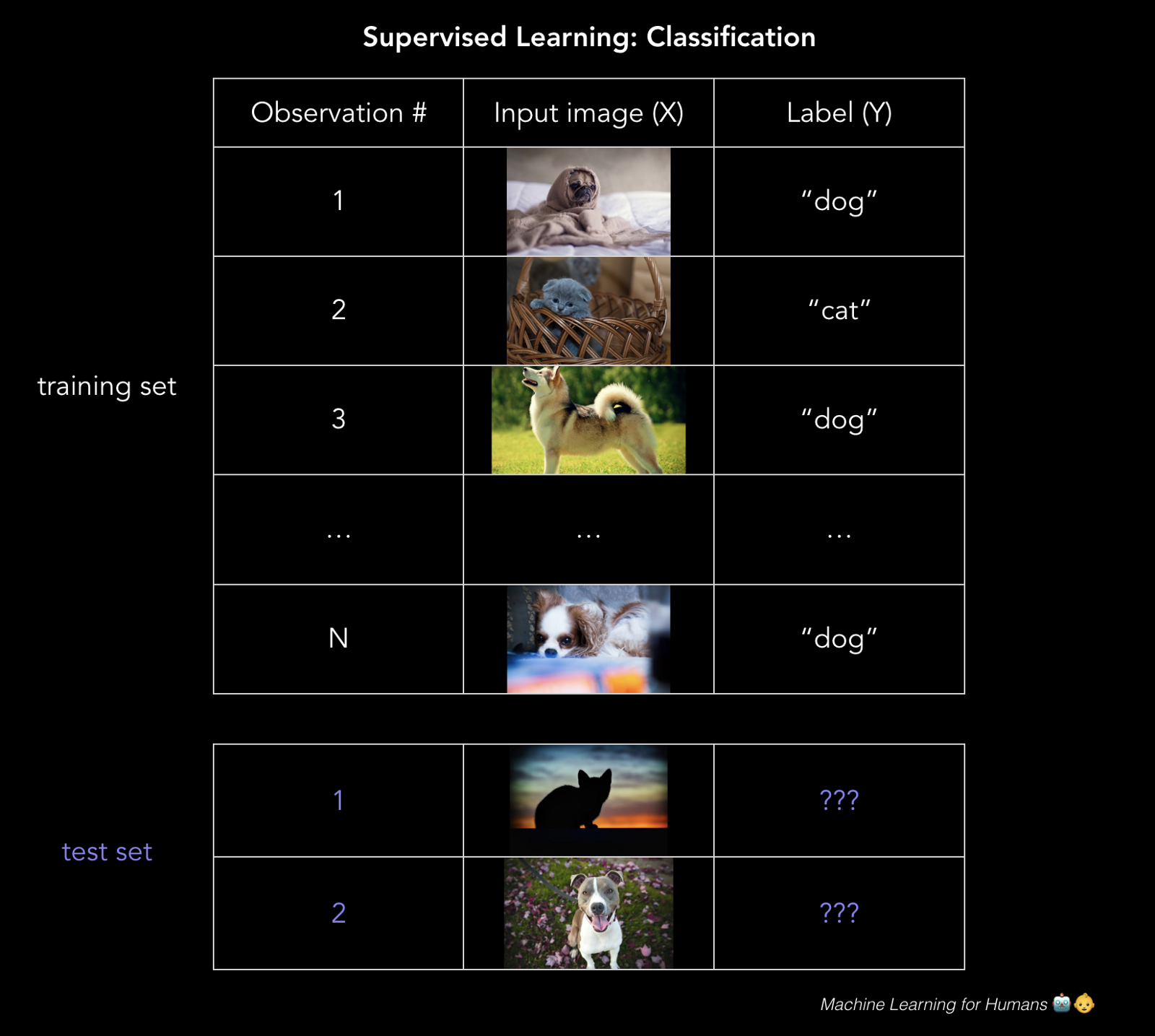
分類：預(yù)測(cè)標(biāo)簽

這個(gè)郵件是不是垃圾郵件猪贪？貸款者能否償還它們的貸款？用戶是否會(huì)點(diǎn)擊廣告川背？你的 Fackbook 照片中那個(gè)人是誰靡砌？

分類預(yù)測(cè)離散的目標(biāo)標(biāo)簽Y授帕。分類是一種問題锋边，將新的觀測(cè)值分配給它們最有可能屬于的類用押，基于從帶標(biāo)簽的訓(xùn)練集中構(gòu)建的模型疯坤。

你的分類的準(zhǔn)確性取決于所選的算法的有效性报慕，你應(yīng)用它的方式，以及你有多少有用的訓(xùn)練數(shù)據(jù)压怠。

對(duì)數(shù)幾率回歸：0 還是 1眠冈？

對(duì)數(shù)幾率（logistic）回歸是個(gè)分類方法：模型輸出目標(biāo)變量Y屬于某個(gè)特定類的概率。

分類的一個(gè)很好的例子是刑峡，判斷貸款申請(qǐng)人是不是騙子洋闽。

最終，出借人想要知道突梦，它們是否應(yīng)該貸給借款人诫舅，以及它們擁有一些容忍度，用于抵抗申請(qǐng)人的確是騙子的風(fēng)險(xiǎn)宫患。這里刊懈，對(duì)數(shù)幾率回歸的目標(biāo)就是計(jì)算申請(qǐng)人是騙子的概率（0%~100%）。使用這些概率娃闲，我們可以設(shè)定一些閾值虚汛，我們?cè)敢饨杞o高于它的借款人，對(duì)于低于它的借款人皇帮，我們拒絕他們的貸款申請(qǐng)卷哩，或者標(biāo)記它們以便后續(xù)觀察。

雖然對(duì)數(shù)幾率回歸通常用于二元分類属拾，其中只存在兩個(gè)類将谊，要注意冷溶，分類可以擁有任意數(shù)量的類（例如，為手寫數(shù)字分配 0~9 的標(biāo)簽尊浓，或者使用人臉識(shí)別來檢測(cè) Fackbook 圖片中是哪個(gè)朋友）逞频。

我可以使用普通最小二乘嘛？

不能栋齿。如果你在大量樣本上訓(xùn)練線性回歸模型苗胀，其中Y = 0或者1，你最后可能預(yù)測(cè)出一些小于 0 或者大于 1 的概率瓦堵，這毫無意義基协。反之，我們使用對(duì)數(shù)幾率回歸模型（或者對(duì)率（logit）模型），它為分配“Y屬于某個(gè)特定類”的概率而設(shè)計(jì)设江，范圍是 0%~100%。

數(shù)學(xué)原理是什么？

注意：這一節(jié)中的數(shù)學(xué)很有意思健田，但是更加技術(shù)化。如果你對(duì)高階的高年不感興趣淑仆，請(qǐng)盡管跳過它漆诽。

對(duì)率模型是個(gè)線性回歸的改良，通過應(yīng)用 sigmoid 函數(shù)扮休，確保輸出 0 和 1 之間的概率迎卤。如果把它畫出來，它就像 S 型的曲線玷坠，稍后可以看到蜗搔。

sigmoid 函數(shù)，它將值壓縮到 0 和 1 之間八堡。

回憶我們的簡單線性回歸模型的原始形式樟凄，我們現(xiàn)在叫它g(X)，因?yàn)槲覀兇蛩阍趶?fù)合函數(shù)中使用它兄渺。

現(xiàn)在缝龄，為了解決模型輸出小于 0 或者大于 1 的問題，我們打算定義一個(gè)新的函數(shù)F(g(X))挂谍，它將現(xiàn)行回歸的輸出壓縮到[0,1]區(qū)間叔壤，來轉(zhuǎn)換g(X)。你可以想到一個(gè)能這樣做的函數(shù)嗎口叙？

你想到了 sigmoid 函數(shù)嗎炼绘？太棒了，這就對(duì)了妄田！

所以我們將g(x)插入 sigmoid 函數(shù)中俺亮，得到了原始函數(shù)的一個(gè)函數(shù)（對(duì)驮捍，事情變得高階了），它輸出 0 和 1 之間的概率铅辞。

換句話說厌漂，我們正在計(jì)算“訓(xùn)練樣本屬于特定類”的概率：P(Y=1)。

這里我們分離了p斟珊，它是Y=1的概率苇倡，在等式左邊。如果我們打算求解等式右邊的囤踩，非常整潔的β0 + β1x + ?旨椒，以便我們能夠直接解釋我們習(xí)得的beta參數(shù)，我們會(huì)得到對(duì)數(shù)幾率比值堵漱，簡稱對(duì)率综慎，它在左邊。這就是“對(duì)率模型”的由來勤庐。

對(duì)數(shù)幾率比值僅僅是概率比值p/(1-p)的自然對(duì)數(shù)示惊，它會(huì)出現(xiàn)在我們每天的對(duì)話中。

在這一季的“權(quán)力的游戲”中愉镰，你認(rèn)為小惡魔掛掉的幾率有多大米罚？

嗯...掛掉的可能性是不掛掉的兩倍。幾率是 2 比 1丈探。的確录择，他太重要，不會(huì)被殺碗降，但是我們都看到了他們對(duì) Ned Stark 做的事情...

要注意在對(duì)率模型中隘竭，β1表示當(dāng)X變化時(shí)，對(duì)率的變化比例讼渊。換句話說动看，它是對(duì)率的斜率，并不是概率的斜率精偿。

對(duì)率可能有點(diǎn)不直觀弧圆，但是值得理解，因?yàn)楫?dāng)你解釋執(zhí)行分類任務(wù)的神經(jīng)網(wǎng)絡(luò)的輸出時(shí)笔咽，它會(huì)再次出現(xiàn)搔预。

使用對(duì)率回歸模型的輸出來做決策

對(duì)率回歸模型的輸出，就像 S 型曲線叶组，基于X的值展示了P(Y=1)拯田。

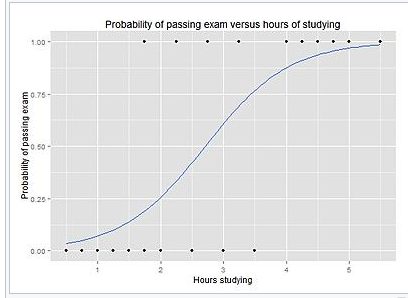
為了預(yù)測(cè)Y標(biāo)簽，是不是垃圾郵件甩十，有沒有癌癥船庇，是不是騙子吭产，以及其他，你需要（為正的結(jié)果）設(shè)置一個(gè)概率截?cái)嘀笛悸郑蛘呓虚撝担ú皇牵┏加佟＠纾绻Ｐ驼J(rèn)為窃爷，郵件是垃圾郵件的概率高于 70%邑蒋，就將其標(biāo)為垃圾。否則就不是垃圾按厘。

這個(gè)閾值取決于你對(duì)假陽性（誤報(bào)）和假陰性（漏報(bào)）的容忍度医吊。如果你在診斷癌癥，你對(duì)假陰性有極低的容忍度逮京，因?yàn)槿绻∪擞袠O小的幾率得癌癥卿堂，你都需要進(jìn)一步的測(cè)試來確認(rèn)。所以你需要為正向結(jié)果設(shè)置一個(gè)很低的閾值懒棉。

另一方面草描，在欺詐性貸款申請(qǐng)的例子中，假陽性的容忍度更高策严，也別是對(duì)于小額貸款陶珠，因?yàn)檫M(jìn)一步的審查開銷很大，并且小額貸款不值得額外的操作成本享钞，以及對(duì)于非欺騙性的申請(qǐng)者來說是個(gè)障礙，它們正在等待進(jìn)一步的處理诀蓉。

對(duì)數(shù)幾率回歸的最小損失

就像線性回歸的例子那樣栗竖，我們使用梯度下降來習(xí)得使損失最小的beta參數(shù)。

在對(duì)率回歸中渠啤，成本函數(shù)是這樣的度量狐肢，當(dāng)真實(shí)答案是0時(shí)，你有多么經(jīng)常將其預(yù)測(cè)為 1沥曹，或者反過來份名。下面是正則化的成本函數(shù)，就像我們對(duì)線性回歸所做的那樣妓美。

當(dāng)你看到像這樣的長式子時(shí)，不要驚慌壶栋。將其拆成小部分，并從概念上思考每個(gè)部分都是什么贵试。之后就能理解了凯正。

第一個(gè)部分是數(shù)據(jù)損失豌蟋，也就是，模型預(yù)測(cè)值和實(shí)際值之間有多少差異梧疲。第二個(gè)部分就是正則損失，也就是往声，我們以什么程度擂找，懲罰模型的較大參數(shù)，它過于看重特定的特征（要記得浩销，這可以阻止過擬合）贯涎。

我們使用低度下降，使損失函數(shù)最小慢洋，就是像上面這樣塘雳。我們構(gòu)建了一個(gè)對(duì)數(shù)幾率回歸模型，來盡可能準(zhǔn)確地預(yù)測(cè)分類普筹。

支持向量機(jī)

我們?cè)俅挝挥谝粋€(gè)充滿彈球的房間里败明。為什么我們總是在充滿彈球的房間里呢？我可以發(fā)誓我已經(jīng)把它們丟掉了太防。

SVM 是我們涉及的最后一個(gè)參數(shù)化模型妻顶。它通常與對(duì)率回歸解決相同的問題，二元分類蜒车，并產(chǎn)生相似的效果讳嘱。它值得理解，因?yàn)樗惴ū举|(zhì)上是由幾何驅(qū)動(dòng)的酿愧，并不是由概率思維驅(qū)動(dòng)的沥潭。

SVM 可解決的一些問題示例：

• 這個(gè)圖片是貓還是狗？
• 這個(gè)評(píng)論是正面還是負(fù)面的嬉挡？
• 二維圖片上的點(diǎn)是紅色還是藍(lán)色钝鸽？

我們使用第三個(gè)例子，來展示 SVM 的工作方式庞钢。像這樣的問題叫做玩具問題拔恰，因?yàn)樗鼈儾皇钦鎸?shí)的。但是沒有東西是真實(shí)的焊夸，所以也沒關(guān)系仁连。

這個(gè)例子中，我們的二維空間中有一些點(diǎn)，它們是紅色或者藍(lán)色的饭冬，并且我們打算將二者干凈地分開使鹅。

訓(xùn)練集畫在了上面的圖片中。我們打算在這個(gè)平面上劃分新的未分類的點(diǎn)昌抠。為了實(shí)現(xiàn)它患朱，SVM 使用分隔直線（在高維里面是個(gè)多維的超平面），將空間分成紅色區(qū)域和藍(lán)色區(qū)域炊苫。你可以想象，分隔直線在上面的圖里面是什么樣执虹。

具體一些袋励，我們?nèi)绾芜x取畫這條線的位置茬故？

下面是這條直線的兩個(gè)示例：

這些圖表使用 MicrosoftPaint 制作磺芭，在不可思議的 32 年之后钾腺，它在幾個(gè)星期之前廢棄了垮庐。R.I.P Paint :(

我希望你擁有一種直覺，覺得第一條線更好逗抑。直線到每一邊的最近的點(diǎn)的距離叫做間距邮府，而 SVM 嘗試使間距最大。你可以將其看做安全空間：空間越大忍啤，嘈雜的點(diǎn)就越不可能被錯(cuò)誤分類。

基于這個(gè)簡單的解釋同波，一個(gè)巨大的問題來了未檩。

(1) 背后的數(shù)學(xué)原理是什么冤狡？

我們打算尋找最優(yōu)超平面（在我們的二維示例中是直線）。這個(gè)超平面需要（1）干凈地分隔數(shù)據(jù)挎峦，將藍(lán)色的點(diǎn)分到一邊坦胶，紅色的點(diǎn)分到另一邊歪玲，以及（2）使間距最大滥崩。這是個(gè)最優(yōu)化問題钙皮。按照（2）的需求使間距最大的時(shí)候，解需要遵循約束（1）导匣。

求解這個(gè)問題的人類版本贡定，就是拿一個(gè)尺子缓待，嘗試不同的直線來分隔所有點(diǎn)渠牲，直到你得到了使間距最大的那條。

人們發(fā)現(xiàn)瘫镇，存在求解這個(gè)最大化的數(shù)學(xué)方式谚咬，但是它超出了我們的范圍通孽。為了進(jìn)一步解釋它背苦，這里是個(gè)視頻講義行剂，使用拉格朗日優(yōu)化展示了它的工作原理。

你最后求解的超平面的定義腌巾，有關(guān)它相對(duì)于特定x_i的位置澈蝙，它們就叫做支持向量灯荧，并且它們通常是最接近超平面的點(diǎn)逗载。

(2) 如果你不能干凈地分隔數(shù)據(jù)链烈，會(huì)發(fā)生什么强衡？

處理這個(gè)問題有兩個(gè)方式。

2.1 軟化“分隔”的定義

我們?cè)试S一些錯(cuò)誤号涯，也就是我們?cè)试S紅色區(qū)域里面有一些藍(lán)色點(diǎn)，或者藍(lán)色區(qū)域里有一些紅色點(diǎn)眉尸。我們向損失函數(shù)中。為錯(cuò)誤分類的樣本添加成本C來實(shí)現(xiàn)霉祸∷坎洌基本上我們說坪蚁，錯(cuò)誤分類是可以接受的贱田，只是會(huì)產(chǎn)生一些成本嘴脾。

2.2 將數(shù)據(jù)放到高維

我們可以創(chuàng)建非線性的分類器译打，通過增加維數(shù)奏司，也就是，包含x^2哥谷，x^3，甚至是cos(x)勉吻，以及其它齿桃。突然短纵，你就有了一個(gè)邊界香到，當(dāng)我們將其帶回低維表示時(shí)，它看起來有些彎曲千绪。

本質(zhì)上盹靴，這就類似紅的和藍(lán)色的彈球都在地面上瑞妇，它們不能用一條直線分隔踪宠。但是如果你讓所有紅色的彈球離開地面，像右圖這樣绍妨，你就能畫一個(gè)平面來分隔它們他去。之后你讓他們落回地面灾测，就知道了藍(lán)色和紅色的邊界媳搪。

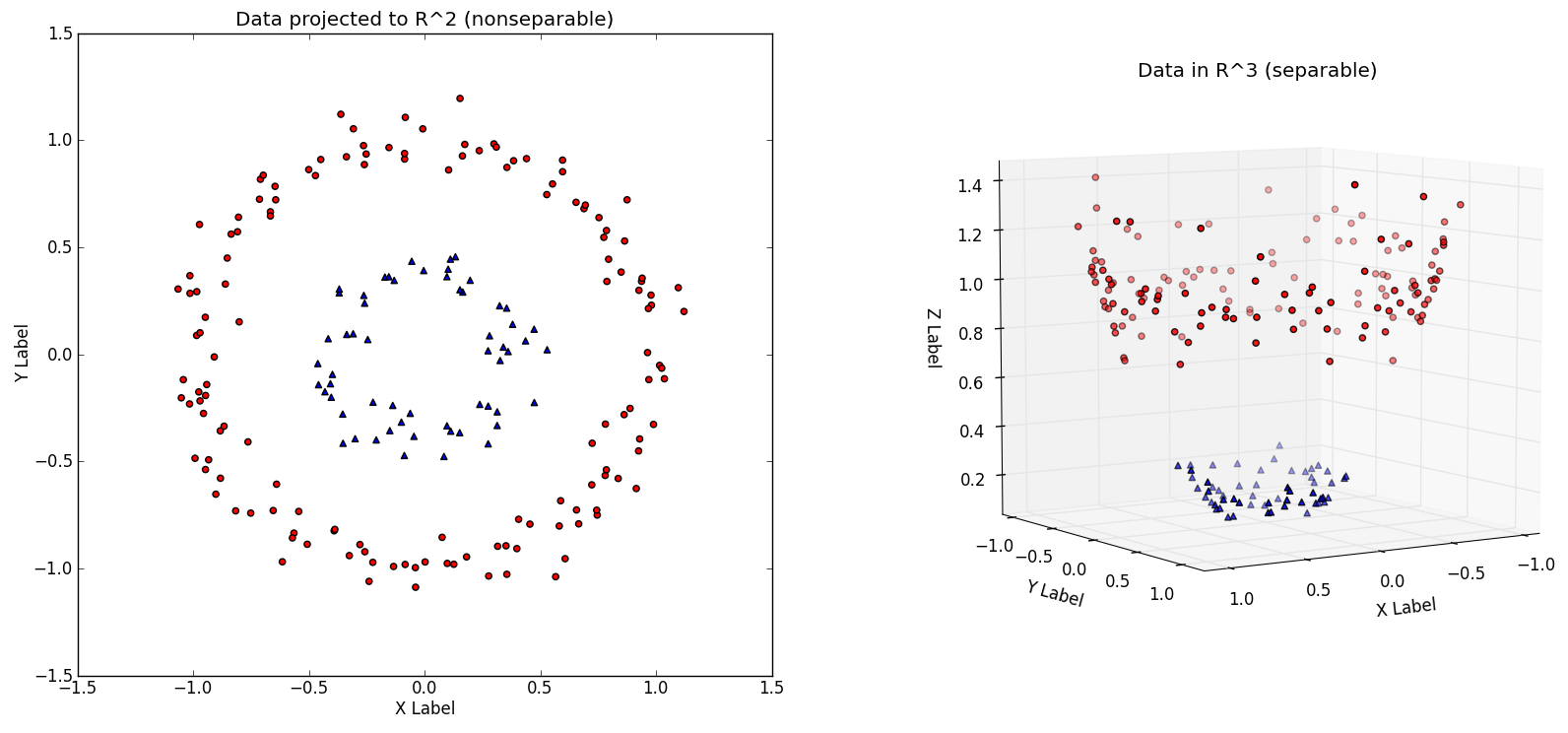
二維空間R^2中的非線性可分的數(shù)據(jù)集秦爆，以及映射到高維的相同數(shù)據(jù)集等限，第三個(gè)維度是x^2+y^2（來源：http://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html）

決策邊界展示為綠色望门，左邊是三維空間，右邊是二維空間锰霜。與上一張來源相同筹误。

總之，SVM 用于二元分類癣缅。它們嘗試尋找一個(gè)平面厨剪，干凈地分隔兩個(gè)類勘畔。如果這不可能，我們可以軟化“分隔”的定義丽惶，或者我們把數(shù)據(jù)放到高維，以便我們可以干凈地分隔數(shù)據(jù)爬立。

好的钾唬！

這一節(jié)中我們涉及了：

• 監(jiān)督學(xué)習(xí)的分類任務(wù)
• 兩種基礎(chǔ)的分類方法：對(duì)數(shù)幾率回歸（LR）和支持向量機(jī)（SVM）
• 常見概念：sigmoid 函數(shù)抡秆，對(duì)數(shù)幾率（對(duì)率）着撩，以及假陽性（誤報(bào)）和假陰性（漏報(bào)）

在“2.3：監(jiān)督學(xué)習(xí) III”中，我們會(huì)深入非參數(shù)化監(jiān)督學(xué)習(xí)，其中算法背后的概念都非常直觀，并且對(duì)于特定類型的問題，表現(xiàn)都很優(yōu)秀，但是模型可能難以解釋。

練習(xí)材料和擴(kuò)展閱讀

2.2a 對(duì)數(shù)幾率回歸

Data School 擁有一個(gè)對(duì)數(shù)幾率回歸的非常棒的深入指南。我們也繼續(xù)向你推薦《An Introduction to Statistical Learning》悬赏。對(duì)數(shù)幾率回歸請(qǐng)見第四章寄锐，支持向量機(jī)請(qǐng)見第九章。

為了解釋對(duì)數(shù)幾率回歸，我們推薦你處理這個(gè)問題集蚕涤。你需要注冊(cè)站點(diǎn)來完成它。很不幸，這就是人生。

2.2b 深入 SVM

為了深入 SVM 背后的數(shù)學(xué)，在 MIT 6.034：人工智能課程中觀看 Patrick Winston 教授的講義茂嗓，并查看這個(gè)教程來完成 Python 實(shí)現(xiàn)蝌矛。