曾梓龍 材料班 2014301020006
前言
最近的研究課題是神經(jīng)網(wǎng)絡,偶然在知乎上看到了一篇關于入門深度學習的文章,介紹了一下從數(shù)學知識到機器學習斩熊,再到神經(jīng)網(wǎng)絡和深度學習的資源里逆,因此開始通過看Andrew Ng的機器學習課程入門機器學習进胯,并在網(wǎng)上在線看Neural Networks and Deep Learning這份線上教程學習神經(jīng)網(wǎng)絡和深度學習。
在花了幾天時間看線上教程原押,我開始著手操作識別手寫數(shù)字圖像的任務胁镐,為了簡化代碼,我使用python構建神經(jīng)網(wǎng)絡诸衔。
背景
首先觀察下面的一副圖片

我們可以很容易地辨識這些數(shù)字是504192盯漂。通過對大腦的研究,我們知道笨农,人類大腦有大約1000億個神經(jīng)元就缆,在這些神經(jīng)元之間有一萬億個鏈接。

而在大腦的每個半球磁餐,人類有一個初級視覺皮層V1违崇,大概有1.4億個神經(jīng)元,以及數(shù)百億的相互連接诊霹,但是人類視覺不僅涉及V1羞延,而且還有V2,V3脾还,V4伴箩,V5這一系列的視覺皮層。

實際上鄙漏,人類大腦就是一臺超級計算機嗤谚,幾百萬年來的調(diào)整和適應使得人類能夠辨識外部世界,因此用計算機模擬書寫數(shù)字是很艱難的怔蚌。
這里有一個問題值得思考巩步。為什么我們能夠辨識手寫數(shù)字9?是因為我們天生就能夠辨識數(shù)字9還是因為我們學習過如何辨識數(shù)字9桦踊?
答案顯然是我們學習過如何辨識并書寫數(shù)字9.
從這個問題出發(fā)來看椅野,我們也可以用計算機模擬人類學習的過程來獲得辨識手寫數(shù)字圖像的能力。
近年來籍胯,神經(jīng)網(wǎng)絡在這類問題的解決上取得了比較大的進展竟闪。而神經(jīng)網(wǎng)絡模擬的就是人類大腦的工作方式——使用大量的訓練數(shù)據(jù)訓練神經(jīng)網(wǎng)絡,使神經(jīng)網(wǎng)絡的從這些數(shù)據(jù)中獲取“經(jīng)驗”杖狼,提高辨識手寫數(shù)字圖像的準確率炼蛤。
何為神經(jīng)網(wǎng)絡以及神經(jīng)網(wǎng)絡的工作原理
Perceptrons(感知器)
在介紹神經(jīng)網(wǎng)絡之前,我們首先需要理解Perceptrons(感知器)的概念蝶涩。Perceptrons實際上就是一個人工模擬的神經(jīng)元理朋,每個感知器有若干個二進制輸入以及一個二進制輸出絮识。

上面的這個Perceptrons有三個輸入:x1、x2和x3嗽上,每條輸入都有相應的權重:w1笋除、w2和w3.
Perceptrons的輸入是由輸入的加權之和決定的,神經(jīng)網(wǎng)絡的研究人員通常用下面的這個公式來確定Perceptrons的輸出:
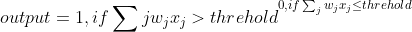
也就是說炸裆,當Perceptrons的輸入加權和大于某一閾值時,輸出1鲜屏;小于某一閾值時輸出0.
這和大腦神經(jīng)元的工作原理比較類似烹看,當神經(jīng)元接收到來自其他神經(jīng)元的信號時,經(jīng)過處理之后再發(fā)送給其他的神經(jīng)元洛史。
在實際應用中惯殊,為了計算方便,我們將上面的式子改為:
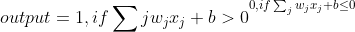
其中:

b為bias.
同時令X為輸入數(shù)據(jù)的矩陣也殖,W為相應的權重矩陣土思,即:
因此輸出表達式為:
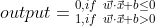
我們在之前也說過,人類大腦識別圖像是通過多層的視覺皮層來解析的信息忆嗜,因此我們這里開始構建一個三層的神經(jīng)網(wǎng)絡:

第一層稱為輸入層己儒,最后一層稱為輸出層,第一層和最后一層之間的層被稱為隱藏層捆毫。
我們首先考慮一下這樣一個Perceptrons闪湾,有兩個輸入端,每個輸入端的權重為-2绩卤,結點bias為3:

如果我們輸入00途样,則有:
(-2)0+(-2)0+3 = 3>0,類似的,輸入為01或者10時輸出都為1濒憋,但是當輸入為11時何暇,輸出為0,因此這樣的一個Perceptrons可以看作一個與非門凛驮。
在數(shù)字邏輯中裆站,我們知道,邏輯門的組合可以組成一定的邏輯開關辐烂,如下圖所示:

將上圖中的與非門換成之前討論的Perceptrons遏插,則有:

減少一些線條,并將輸入端轉換為Perceptrons纠修,則有:

從上面的例子可以看到胳嘲,不同的Perceptrons的組合網(wǎng)絡可以具有一定的邏輯功能,利用神經(jīng)網(wǎng)絡識別手寫數(shù)字也是一樣的原理扣草。
Sigmod 神經(jīng)元
在實際應用中了牛,并不會使用之前介紹的Perceptrons組成的神經(jīng)網(wǎng)絡颜屠,那樣構建的神經(jīng)網(wǎng)絡不夠穩(wěn)定,在使用訓練集訓練網(wǎng)絡的時候網(wǎng)絡權重鹰祸、bias甚至網(wǎng)絡的輸出的變化非常大甫窟。因此,往往使用Sigmod神經(jīng)元蛙婴。
Sigmod神經(jīng)元里的Perceptrons和之前的Perceptrons并無兩樣粗井,但是Perceptrons的輸出output的值并非0或1,相反街图,output 為:
)
其中σ稱為sigmoid函數(shù)浇衬,sigmoid函數(shù)定義如下:
\equiv \frac{1}{1+e^{-z}}.)
因此對于輸入為x1,x2,...,輸入權重為w1,w2,...,且bias為b時,sigmoid神經(jīng)元的輸出為:
sigmoid函數(shù)σ(z)的圖像如下圖所示:

當z大于0時餐济,sigmoid函數(shù)小于1大于0.5耘擂,當z小于0時,sigmoid函數(shù)大于0小于0.5.

這是之前剛開始介紹的Perceptrons的輸出函數(shù)(Step function)的圖像
sigmoid function與step function相比更為平滑絮姆,當權重w醉冤、bias b有微小變化時,sigmoid函數(shù)的輸出的變化也很微小篙悯。因此一般采用sigmoid函數(shù)作為輸出函數(shù)蚁阳。
從sigmoid函數(shù)圖像可以看到,sigmoid函數(shù)的輸出是連續(xù)變化的辕近,可能是0.173或者0.689韵吨,那么如何界定sigmoid的輸出值以確定output值?
我們一般界定移宅,當sigmoid函數(shù)大于0.5時output為1归粉,當sigmoid函數(shù)小于0.5時,output為0
識別手寫數(shù)字的神經(jīng)網(wǎng)絡搭建
首先漏峰,我們識別一個手寫數(shù)字:

為了識別單個數(shù)字糠悼,我們使用一個三層的神經(jīng)網(wǎng)絡:

由于我們的手寫數(shù)字是一個28*28的像素的圖像,因此手寫數(shù)字圖像中一共有784個像素浅乔,這些像素塊經(jīng)過編碼后輸入到神經(jīng)網(wǎng)絡中倔喂,因此這個三層神經(jīng)網(wǎng)絡的輸入端有784個神經(jīng)元。
輸入端值為1時代表像素塊為1靖苇,值為0時代表像素塊為白色席噩,當輸入端值介于0到1之間時,代表深度不同的灰色贤壁。
第二層也就是隱藏層悼枢,在圖中僅有15個神經(jīng)元,不過在實際情況中有可能不只15個神經(jīng)元脾拆。
第三層也就是輸出層馒索,有十個神經(jīng)元莹妒,如果哪個神經(jīng)元輸出為1,則代表神經(jīng)網(wǎng)絡認定輸入的圖像為相應的數(shù)字绰上。例如旨怠,如果第一個神經(jīng)元輸出為1,則神經(jīng)網(wǎng)絡認定輸入的手寫數(shù)字為0.
梯度下降算法
之前我們說過蜈块,神經(jīng)網(wǎng)絡可以通過訓練數(shù)據(jù)集來獲得辨識圖像的能力鉴腻,其模擬的就是人類的學習能力,在這里我們提出一個梯度下降學習算法模擬學習的過程百揭。
我們使用向量x表示輸入的值拘哨,則x是一個784維度的向量,輸入端用y表示信峻,則有
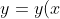)
其中,y是一個10維的向量瓮床。
舉個例子來說盹舞,如果一個訓練圖像被神經(jīng)網(wǎng)絡認定為6,則
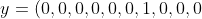^T)
就是神經(jīng)網(wǎng)絡的輸出向量隘庄。
為了不斷調(diào)整神經(jīng)網(wǎng)絡內(nèi)的權重和bias踢步,我們提出梯度下降算法,首先定義一個代價函數(shù):
 \equiv \frac{1}{2n}\sum_x ||y(x)-a||^2)
其中w為神經(jīng)網(wǎng)絡中所有的權重值丑掺,b為所有的bias获印,n為輸入的訓練集的數(shù)量,a是當輸入為x時神經(jīng)網(wǎng)絡的輸出向量街州。由此可見兼丰,w、b和n為a的自變量唆缴。

如上圖為代價函數(shù)C(w,b)的等勢圖鳍征,中心處為代價函數(shù)圖像的最低點,越往外面徽,點所處的位置越高艳丛。因此為了求得代價函數(shù)C的極小值,我們需要找到相應代價函數(shù)的圖像的最低點趟紊。

更直觀一點就像上面這幅圖所示氮双,小球處于某一位置,總有向最低點運動的趨勢霎匈。為了在數(shù)學語言上描述這一過程戴差,我們提出梯度下降算法:

令:
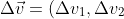^T)
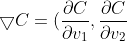)
有:

因為代價函數(shù)需要沿梯度下降,所以應當有

令:
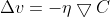
其中唧躲,η是一個很小的正參數(shù):

更新參數(shù)v造挽,有:
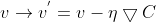
因此碱璃,分別更新權重w和偏重b:
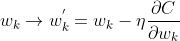
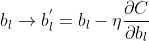
但是在實際情況中,使用梯度下降學習算法訓練神經(jīng)網(wǎng)絡效率比較低饭入,因此我們采用隨機梯度下降學習算法嵌器。
隨機梯度下降學習算法的基本思想是在所有訓練集中隨機挑選m個訓練集輸入到神經(jīng)網(wǎng)絡中進行訓練,m足夠大以至于可以認為這m個訓練集的訓練效果相當于所有訓練集訓練神經(jīng)網(wǎng)絡的效果谐丢,用數(shù)學公式表達就是:
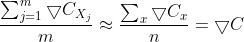
也就是說爽航,w與b的更新函數(shù)可以改為:
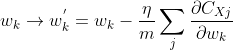
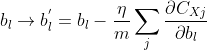
編程實現(xiàn)
先建立一個Network類:
class Network(self):
def __init__(self,sizes):
self.num_layers = len(sizes)
self.sizes = sizes
# if we want to create a Network object with 2 neurons
# in the first layer,3 neurons in the second layer,and
# 1 neurons in the final layer,we can do this in this
# code:
# net = Network([2,3,1])
self.biases = [np.random.randn(y,1) for y in sizes[1:]]
self.weights = [np.random.randn(y,x)
for x,y in zip(sizes[:-1],sizes[1:])]
我們建立的是一個三層的神經(jīng)網(wǎng)絡,傳入一個三維的向量,例如:
如果我們想在輸入層放入2個神經(jīng)元乾忱,隱藏層放入3個神經(jīng)元讥珍,輸出層放入1個神經(jīng)元,則將[2,3,1]傳入神經(jīng)網(wǎng)絡中窄瘟。
net = Network([2,3,1])
biases和weight則先用random函數(shù)初始化衷佃,隨機設置。
定義sigmoid函數(shù):
def sigmod(z):
return 1.0/(1.0+np.exp(-z))
每一層神經(jīng)元的輸出由上一層神經(jīng)元的輸入決定蹄葱,由數(shù)學公式表達就是:
其中氏义,a是上一層神經(jīng)元的輸出,即這一神經(jīng)元的輸入图云,w是相應兩層神經(jīng)元之間的權重向量惯悠。
同時在Network類中定義feedforward方法:
def feedforward(self,a):
for b,w in zip(self.biases,self.weights):
a = sigmod(np.dot(w,a)+b)
return a
同時在Network類中定義SGD方法,SGD方法使神經(jīng)網(wǎng)絡能夠使用隨機梯度下降算法進行學習:
def SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):
# epochs:the number of epochs to train for
# mini_batch_size:the size of the mini-batches to use
# when sampling.eta is the learning rate /eta.
if test_data:
n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0,n,mini_batch_size)]
# catch k in every mini_batch_size
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch,eta)
if test_data:
print("Epoch {0}:{1}/{2}".format(j,self.evaluate(test_data),n_test))
else:
print("Epoch {0} complete".format(j))
在之前討論隨機梯度下降學習算法的時候竣况,我們談到w與b要隨神經(jīng)網(wǎng)絡的學習不斷更新克婶,在這里定義一個update_mini_batch方法:
def update_mini_batch(self,mini_batch,eta):
# update the network's weights and biases by applying gradient
# descent using backpropagation to a single mini batch
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x,y in mini_batch:
delta_nabla_b,delta_nabla_w = self.backprop(x,y)
nabla_b = [nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]
nabla_w = [nw+dnw for nw,dnw in zip(nabla_w,delta_nabla_w)]
self.weights = [w-((eta)/len(mini_batch))*nw
for w,nw in zip(self.weights,nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b,nb in zip(self.biases,nabla_b)]
完整代碼已經(jīng)托管到github上了。
在使用神經(jīng)網(wǎng)絡的時候丹泉,還需要一個python文件將訓練集輸入到神經(jīng)網(wǎng)絡中情萤,我使用了國外某大佬的mnist_loader.py文件,也托管在github上了摹恨。
運行操作
打開python shell紫岩,切換到程序文件目錄,輸入下列代碼:

在進入python交互環(huán)境之后睬塌,第一行和第二行代碼導入了訓練集泉蝌,第三行和第四行代碼創(chuàng)建了一個第一層為784個神經(jīng)元 第二層為30個神經(jīng)元 第三層為10個神經(jīng)元的神經(jīng)網(wǎng)絡。
再輸入下列這行代碼啟動神經(jīng)網(wǎng)絡:
net.SGD(training_data,30,10,3.0,test_data=test_data)
這行代碼的意思是訓練30次揩晴,同時挑選10組訓練集作為隨機梯度下降算法的訓練集勋陪,學習速率η為3.0,運行一段時間后硫兰,得到:

經(jīng)過30次訓練之后诅愚,神經(jīng)網(wǎng)絡辨識圖像的準確度可以達到94.89%,實際上在第28次訓練的時候準確度已經(jīng)達到了94.99%.
如果我們將這個神經(jīng)網(wǎng)絡的第二層改為100個神經(jīng)元,神經(jīng)網(wǎng)絡的辨識度可以達到多少劫映?
輸入下列代碼:
net = network.Network([784,100,10])
啟動神經(jīng)網(wǎng)絡违孝,我們可以將神經(jīng)網(wǎng)絡的辨識率提高到96%以上刹前。
重新回到第二層為30個神經(jīng)元的情況上,如果將學習速率η提高到20的話雌桑,將程序運行一遍得到:

可以發(fā)現(xiàn)喇喉,神經(jīng)網(wǎng)絡辨識圖像的準確率有所下降。
總結
訓練神經(jīng)網(wǎng)絡所需的計算量十分巨大校坑,用普通的筆記本運行整個程序需要花費比較長的一段時間拣技,因此,在實際應用中一般采用GPU來訓練神經(jīng)網(wǎng)絡耍目。在實際模擬的過程中膏斤,我們可以發(fā)現(xiàn),神經(jīng)網(wǎng)絡的辨識率雖然可以提高到95%以上邪驮,但是在這之后其辨識率很難得到提高莫辨,這迫使我們不斷發(fā)展神經(jīng)網(wǎng)絡模型。