一.
Investigate the Lyapunov exponent of the stadium billiard for several values of
. You can do this qualitatively by examining the behavior for only one set of initial conditions for each value of you consider, or more quantitatively by averaging over a range of initial conditions for each value of.
二.
臺(tái)球動(dòng)力系統(tǒng)是一個(gè)粒子沿直線勻速運(yùn)動(dòng)并在邊界發(fā)生鏡面反射的動(dòng)力系統(tǒng)勾缭。當(dāng)粒子擊中邊界發(fā)生反射時(shí)它不會(huì)損失動(dòng)能。臺(tái)球動(dòng)力系統(tǒng)是哈密頓理想化的臺(tái)球游戲,但其邊界可以是矩形等其他形狀,甚至可以是多維的想括。臺(tái)球動(dòng)力系統(tǒng)也可以被用于研究非歐幾何。
臺(tái)球動(dòng)力系統(tǒng)擁有哈密頓系統(tǒng)從可積性到混沌運(yùn)動(dòng)的所有復(fù)雜性牢撼,無(wú)須對(duì)運(yùn)動(dòng)方程進(jìn)行困難的積分就可確定其龐加萊截面淮逻。喬治·大衛(wèi)·比爾霍夫證明一個(gè)橢圓邊界的臺(tái)球動(dòng)力系統(tǒng)是可積的。
三.模擬
-
理論推導(dǎo)
速度分解:
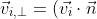\vec n)
撞擊邊界:
算法
用歐勒法進(jìn)行模擬結(jié)果模擬



- 動(dòng)圖演示
