初中學(xué)了簡(jiǎn)單了胡克定律剃根,高中的時(shí)候力變成了向量,而大學(xué)里應(yīng)力應(yīng)變都變成了2階張量前方,同樣是胡克定律狈醉,在不同的尺度下,卻有不同的含義惠险。
標(biāo)量尺度
我們初中學(xué)過胡克定律苗傅,即在彈性范圍內(nèi),彈簧的伸長(zhǎng)和所施加的力成正比:

用公式表達(dá)就是:

這里k是一個(gè)實(shí)數(shù)班巩,表明了彈簧的性質(zhì)渣慕,當(dāng)彈簧壓縮時(shí),該式任然成立抱慌,只是F和X前面變成了負(fù)號(hào)逊桦。
向量尺度
高中時(shí),力F變成了向量遥缕,位移X也變成了向量卫袒,什么是向量?既有大小又有方向的量就是向量单匣,和標(biāo)量尺度的胡克定律比較夕凝,引進(jìn)向量其實(shí)就是引進(jìn)了方向,但是各個(gè)方向上任然滿足標(biāo)量形式的胡克定律户秤,胡克定律的公式?jīng)]變码秉,只是其中的F和X是向量了,這時(shí)如果將胡克定律在直角坐標(biāo)系下展開:

即:
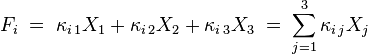
其中i從1到3.
所以鸡号,胡克定律:

任然成立转砖,只是這里的F和X是向量,而kappa不再是一個(gè)實(shí)數(shù)(標(biāo)量)鲸伴,而是一個(gè)2階張量府蔗。
張量尺度
在大學(xué)里學(xué)了連續(xù)介質(zhì)力學(xué),這時(shí)的胡克定律變成了:
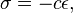
其中sigma是應(yīng)力張量(2階)汞窗,epsilon是應(yīng)變張量(2階)姓赤,而c是一個(gè)剛度張量(4階)
在直角坐標(biāo)系下,應(yīng)力張量和應(yīng)變張量可以表示為矩陣的形式:
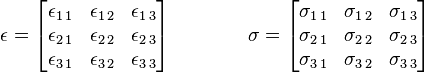
而4階的剛度張量在直角坐標(biāo)系下:

一共有3*3*3*3=81個(gè)元素仲吏。
所以直角坐標(biāo)系下的胡克定律可以寫為:

剛度張量的簡(jiǎn)化
有以上可知不铆,剛度張量有3*3*3*3=81個(gè)元素蝌焚,那能不能將他簡(jiǎn)化呢?
小的對(duì)稱minor symmetries
由于柯西應(yīng)力張量的對(duì)稱性:

我們可以得到:

同樣的誓斥,由于應(yīng)變張量的對(duì)稱性只洒,我們可以得到:

這樣剛度張量的元素個(gè)數(shù)就從81個(gè)減小到了36個(gè)。
在直角坐標(biāo)系下劳坑,這時(shí)的應(yīng)力應(yīng)變張量可以表示為:

而剛度張量的36個(gè)元素可以表示為:

注意:由于對(duì)稱性毕谴,這時(shí)的剛度張量已從4階變成了2階。
大的對(duì)稱major symmetries
由于應(yīng)力應(yīng)變張量同時(shí)變化泡垃,應(yīng)力應(yīng)變關(guān)系可以從應(yīng)變能量密度(U)的微分得到:

由于積分順序的任意性析珊,我們可以得到:

這樣剛度張量的元素個(gè)數(shù)就從36個(gè)減小到了21個(gè)。
在直角坐標(biāo)系下蔑穴,這時(shí)的剛度張量的矩陣表示:

是一個(gè)對(duì)稱矩陣忠寻,所以只有6+5+4+3+2+1=21個(gè)元素。
其他對(duì)稱性
以上的兩種對(duì)稱一般的材料都會(huì)有存和,而接下來的這些對(duì)稱性確是只有在特定條件下才能滿足:

正交對(duì)稱Orthotropic
正交對(duì)稱有兩個(gè)對(duì)稱面(可以證明:有兩個(gè)對(duì)稱面一定會(huì)有第三個(gè))奕剃,典型的正交對(duì)稱材料是木頭

木頭的性質(zhì)沿著半徑方向,圓周方向以及軸向是不同的捐腿。
在直角坐標(biāo)系下纵朋,如果坐標(biāo)基矢量e1,e2茄袖,e3垂直于3個(gè)對(duì)稱面操软,那么剛度張量元素個(gè)數(shù)可以從21個(gè)減小到9個(gè):

橫斷對(duì)稱Transversely isotropic
橫斷對(duì)稱有一個(gè)對(duì)稱軸,很多復(fù)合材料和生物薄膜材料都是橫斷對(duì)稱的宪祥。
在直角坐標(biāo)系下聂薪,如果坐標(biāo)基矢量e3和對(duì)稱軸重合,那么剛度張量元素個(gè)數(shù)可以進(jìn)一步從9個(gè)減小到5個(gè):

立方對(duì)稱cubic symmetry
立方對(duì)稱是最簡(jiǎn)單的各向異性情況,這時(shí)剛度矩陣元素個(gè)數(shù)為3個(gè):

各向同性isotropic
終于到了各向同性蝗羊,這一我們最常應(yīng)用的情況藏澳,各向同性的材料,顧名思義耀找,材料在各個(gè)方向上的性質(zhì)是一樣的翔悠,也可以說它有無窮多個(gè)對(duì)稱面。各向同性的材料野芒,剛度矩陣元素個(gè)數(shù)為2蓄愁。
在直角坐標(biāo)系下,公式表示為:

矩陣表示為:

其中狞悲,lamda等于:
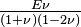
u等于:

所以上式變?yōu)椋?/p>

總結(jié)
仿佛坐了一次過山車涝登,從初中學(xué)過的最簡(jiǎn)單形式的胡克定律開始(此時(shí)彈性系數(shù)k為一實(shí)數(shù)),到向量形式的胡克定律(此時(shí)k為一2階張量效诅,含9個(gè)元素)胀滚,最后到連續(xù)介質(zhì)力學(xué)中張量形式的胡克定律(此時(shí)k為一4階張量,含81個(gè)元素)乱投,然后由于對(duì)稱性咽笼,元素個(gè)數(shù)不斷減少,在各向同性材料里戚炫,k只有兩個(gè)元素剑刑。從中可以看出,升階其實(shí)就是將更多方向性考慮進(jìn)去双肤,這樣就需要更多的元素表示不同的方向施掏,而對(duì)稱性又決定了我們可以用同一元素代表不同方向的性質(zhì)。我們從“1”出發(fā)茅糜,最后回到了“2”七芭。
參考文獻(xiàn)
wikipedia_Hooke's law
Linear elasticity
Orthotropic material