分類:DL2013-07-19 20:18788人閱讀評(píng)論(0)收藏舉報(bào)
轉(zhuǎn)自u(píng)fldl罗晕,原文地址:http://deeplearning.stanford.edu/wiki/index.php/%E8%87%AA%E7%BC%96%E7%A0%81%E7%AE%97%E6%B3%95%E4%B8%8E%E7%A8%80%E7%96%8F%E6%80%A7

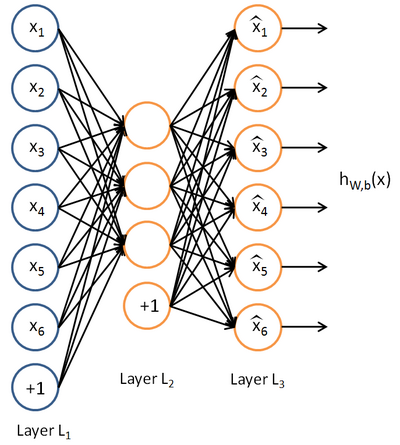
目前為止,我們已經(jīng)討論了神經(jīng)網(wǎng)絡(luò)在有監(jiān)督學(xué)習(xí)中的應(yīng)用肩钠。在有監(jiān)督學(xué)習(xí)中碾褂,訓(xùn)練樣本是有類別標(biāo)簽的∈藜洌現(xiàn)在假設(shè)我們只有一個(gè)沒有帶類別標(biāo)簽的訓(xùn)練樣本集合



自編碼神經(jīng)網(wǎng)絡(luò)嘗試學(xué)習(xí)一個(gè)










我們剛才的論述是基于隱藏神經(jīng)元數(shù)量較小的假設(shè)。但是即使隱藏神經(jīng)元的數(shù)量較大(可能比輸入像素的個(gè)數(shù)還要多)勿侯,我們?nèi)匀煌ㄟ^給自編碼神經(jīng)網(wǎng)絡(luò)施加一些其他的限制條件來發(fā)現(xiàn)輸入數(shù)據(jù)中的結(jié)構(gòu)拓瞪。具體來說,如果我們給隱藏神經(jīng)元加入稀疏性限制助琐,那么自編碼神經(jīng)網(wǎng)絡(luò)即使在隱藏神經(jīng)元數(shù)量較多的情況下仍然可以發(fā)現(xiàn)輸入數(shù)據(jù)中一些有趣的結(jié)構(gòu)吴藻。
稀疏性可以被簡單地解釋如下。如果當(dāng)神經(jīng)元的輸出接近于1的時(shí)候我們認(rèn)為它被激活弓柱,而輸出接近于0的時(shí)候認(rèn)為它被抑制沟堡,那么使得神經(jīng)元大部分的時(shí)間都是被抑制的限制則被稱作稀疏性限制。這里我們假設(shè)的神經(jīng)元的激活函數(shù)是sigmoid函數(shù)矢空。如果你使用tanh作為激活函數(shù)的話航罗,當(dāng)神經(jīng)元輸出為-1的時(shí)候,我們認(rèn)為神經(jīng)元是被抑制的屁药。






注意到表示隱藏神經(jīng)元的激活度粥血,但是這一表示方法中并未明確指出哪一個(gè)輸入帶來了這一激活度。所以我們將使用來表示在給定輸入為情況下酿箭,自編碼神經(jīng)網(wǎng)絡(luò)隱藏神經(jīng)元的激活度复亏。 進(jìn)一步,讓



表示隱藏神經(jīng)元的平均活躍度(在訓(xùn)練集上取平均)缭嫡。我們可以近似的加入一條限制

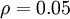



為了實(shí)現(xiàn)這一限制,我們將會(huì)在我們的優(yōu)化目標(biāo)函數(shù)中加入一個(gè)額外的懲罰因子纵诞,而這一懲罰因子將懲罰那些和有顯著不同的情況從而使得隱藏神經(jīng)元的平均活躍度保持在較小范圍內(nèi)上祈。懲罰因子的具體形式有很多種合理的選擇,我們將會(huì)選擇以下這一種:




這里浙芙,是隱藏層中隱藏神經(jīng)元的數(shù)量登刺,而索引依次代表隱藏層中的每一個(gè)神經(jīng)元。如果你對(duì)相對(duì)熵(KL divergence)比較熟悉茁裙,這一懲罰因子實(shí)際上是基于它的塘砸。于是懲罰因子也可以被表示為
其中








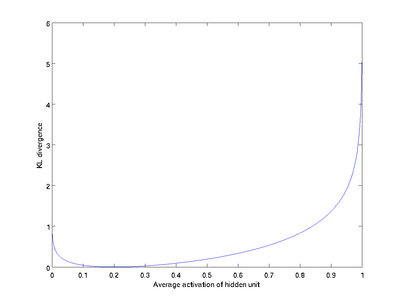
這一懲罰因子有如下性質(zhì)女轿,當(dāng)時(shí),并且隨著與之間的差異增大而單調(diào)遞增壕翩。舉例來說蛉迹,在下圖中,我們?cè)O(shè)定并且畫出了相對(duì)熵值


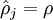




我們可以看出北救,相對(duì)熵在時(shí)達(dá)到它的最小值0,而當(dāng)靠近0或者1的時(shí)候芜抒,相對(duì)熵則變得非常大(其實(shí)是趨向于)珍策。所以,最小化這一懲罰因子具有使得靠近的效果宅倒。 現(xiàn)在攘宙,我們的總體代價(jià)函數(shù)可以表示為






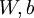
其中如之前所定義,而控制稀疏性懲罰因子的權(quán)重拐迁。項(xiàng)則也(間接地)取決于蹭劈,因?yàn)樗请[藏神經(jīng)元的平均激活度,而隱藏層神經(jīng)元的激活度取決于线召。
為了對(duì)相對(duì)熵進(jìn)行導(dǎo)數(shù)計(jì)算铺韧,我們可以使用一個(gè)易于實(shí)現(xiàn)的技巧,這只需要在你的程序中稍作改動(dòng)即可缓淹。具體來說祟蚀,前面在后向傳播算法中計(jì)算第二層()更新的時(shí)候我們已經(jīng)計(jì)算了
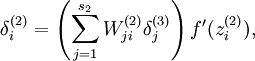
現(xiàn)在我們將其換成

就可以了。
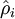
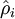

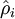
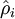
有一個(gè)需要注意的地方就是我們需要知道來計(jì)算這一項(xiàng)更新割卖。所以在計(jì)算任何神經(jīng)元的后向傳播之前前酿,你需要對(duì)所有的訓(xùn)練樣本計(jì)算一遍前向傳播,從而獲取平均激活度鹏溯。如果你的訓(xùn)練樣本可以小到被整個(gè)存到內(nèi)存之中(對(duì)于編程作業(yè)來說罢维,通常如此),你可以方便地在你所有的樣本上計(jì)算前向傳播并將得到的激活度存入內(nèi)存并且計(jì)算平均激活度 丙挽。然后你就可以使用事先計(jì)算好的激活度來對(duì)所有的訓(xùn)練樣本進(jìn)行后向傳播的計(jì)算肺孵。如果你的數(shù)據(jù)量太大,無法全部存入內(nèi)存颜阐,你就可以掃過你的訓(xùn)練樣本并計(jì)算一次前向傳播平窘,然后將獲得的結(jié)果累積起來并計(jì)算平均激活度(當(dāng)某一個(gè)前向傳播的結(jié)果中的激活度被用于計(jì)算平均激活度之后就可以將此結(jié)果刪除)。然后當(dāng)你完成平均激活度的計(jì)算之后凳怨,你需要重新對(duì)每一個(gè)訓(xùn)練樣本做一次前向傳播從而可以對(duì)其進(jìn)行后向傳播的計(jì)算瑰艘。對(duì)于后一種情況是鬼,你對(duì)每一個(gè)訓(xùn)練樣本需要計(jì)算兩次前向傳播,所以在計(jì)算上的效率會(huì)稍低一些紫新。
證明上面算法能達(dá)到梯度下降效果的完整推導(dǎo)過程不再本教程的范圍之內(nèi)均蜜。不過如果你想要使用經(jīng)過以上修改的后向傳播來實(shí)現(xiàn)自編碼神經(jīng)網(wǎng)絡(luò),那么你就會(huì)對(duì)目標(biāo)函數(shù)

自編碼算法 Autoencoders
稀疏性 Sparsity
神經(jīng)網(wǎng)絡(luò) neural networks
監(jiān)督學(xué)習(xí) supervised learning
無監(jiān)督學(xué)習(xí) unsupervised learning
反向傳播算法 backpropagation
隱藏神經(jīng)元 hidden units
像素灰度值 the pixel intensity value
獨(dú)立同分布 IID
主元分析 PCA
激活 active
抑制 inactive
激活函數(shù) activation function
激活度 activation
平均活躍度 the average activation
稀疏性參數(shù) sparsity parameter
懲罰因子 penalty term
相對(duì)熵 KL divergence
伯努利隨機(jī)變量 Bernoulli random variable
總體代價(jià)函數(shù) overall cost function
后向傳播 backpropagation
前向傳播 forward pass
梯度下降 gradient descent
目標(biāo)函數(shù) the objective
梯度驗(yàn)證方法 the derivative checking method
周韜(ztsailing@gmail.com)充择,葛燕儒(yrgehi@gmail.com),林鋒(xlfg@yeah.net)匪蟀,余凱(kai.yu.cool@gmail.com)
目前為止聪铺,我們已經(jīng)討論了神經(jīng)網(wǎng)絡(luò)在有監(jiān)督學(xué)習(xí)中的應(yīng)用。在有監(jiān)督學(xué)習(xí)中萄窜,訓(xùn)練樣本是有類別標(biāo)簽的×逄蓿現(xiàn)在假設(shè)我們只有一個(gè)沒有帶類別標(biāo)簽的訓(xùn)練樣本集合
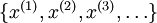
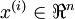
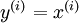
自編碼神經(jīng)網(wǎng)絡(luò)嘗試學(xué)習(xí)一個(gè)
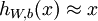
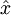


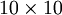
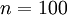
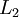
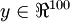
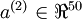

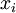
我們剛才的論述是基于隱藏神經(jīng)元數(shù)量較小的假設(shè)蹭睡。但是即使隱藏神經(jīng)元的數(shù)量較大(可能比輸入像素的個(gè)數(shù)還要多)衍菱,我們?nèi)匀煌ㄟ^給自編碼神經(jīng)網(wǎng)絡(luò)施加一些其他的限制條件來發(fā)現(xiàn)輸入數(shù)據(jù)中的結(jié)構(gòu)。具體來說肩豁,如果我們給隱藏神經(jīng)元加入稀疏性限制脊串,那么自編碼神經(jīng)網(wǎng)絡(luò)即使在隱藏神經(jīng)元數(shù)量較多的情況下仍然可以發(fā)現(xiàn)輸入數(shù)據(jù)中一些有趣的結(jié)構(gòu)。
稀疏性可以被簡單地解釋如下清钥。如果當(dāng)神經(jīng)元的輸出接近于1的時(shí)候我們認(rèn)為它被激活琼锋,而輸出接近于0的時(shí)候認(rèn)為它被抑制,那么使得神經(jīng)元大部分的時(shí)間都是被抑制的限制則被稱作稀疏性限制祟昭。這里我們假設(shè)的神經(jīng)元的激活函數(shù)是sigmoid函數(shù)缕坎。如果你使用tanh作為激活函數(shù)的話,當(dāng)神經(jīng)元輸出為-1的時(shí)候篡悟,我們認(rèn)為神經(jīng)元是被抑制的谜叹。
注意到
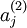


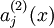


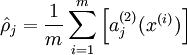
表示隱藏神經(jīng)元

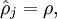
其中忙厌,

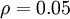

為了實(shí)現(xiàn)這一限制,我們將會(huì)在我們的優(yōu)化目標(biāo)函數(shù)中加入一個(gè)額外的懲罰因子勿璃,而這一懲罰因子將懲罰那些


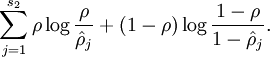
這里,
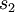

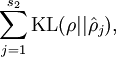
其中
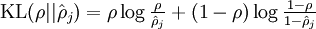


這一懲罰因子有如下性質(zhì)邪码,當(dāng)
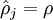
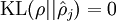


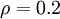
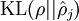

我們可以看出影钉,相對(duì)熵在
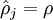

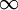


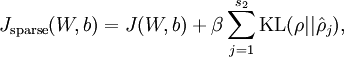
其中
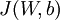
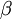

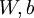

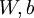
為了對(duì)相對(duì)熵進(jìn)行導(dǎo)數(shù)計(jì)算岗照,我們可以使用一個(gè)易于實(shí)現(xiàn)的技巧村象,這只需要在你的程序中稍作改動(dòng)即可。具體來說攒至,前面在后向傳播算法中計(jì)算第二層(
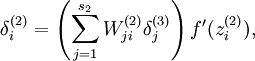
現(xiàn)在我們將其換成
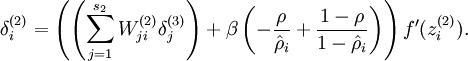
就可以了厚者。
有一個(gè)需要注意的地方就是我們需要知道
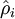
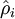
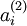
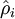
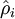
證明上面算法能達(dá)到梯度下降效果的完整推導(dǎo)過程不再本教程的范圍之內(nèi)吨铸。不過如果你想要使用經(jīng)過以上修改的后向傳播來實(shí)現(xiàn)自編碼神經(jīng)網(wǎng)絡(luò),那么你就會(huì)對(duì)目標(biāo)函數(shù)
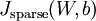
自編碼算法 Autoencoders
稀疏性 Sparsity
神經(jīng)網(wǎng)絡(luò) neural networks
監(jiān)督學(xué)習(xí) supervised learning
無監(jiān)督學(xué)習(xí) unsupervised learning
反向傳播算法 backpropagation
隱藏神經(jīng)元 hidden units
像素灰度值 the pixel intensity value
獨(dú)立同分布 IID
主元分析 PCA
激活 active
抑制 inactive
激活函數(shù) activation function
激活度 activation
平均活躍度 the average activation
稀疏性參數(shù) sparsity parameter
懲罰因子 penalty term
相對(duì)熵 KL divergence
伯努利隨機(jī)變量 Bernoulli random variable
總體代價(jià)函數(shù) overall cost function
后向傳播 backpropagation
前向傳播 forward pass
梯度下降 gradient descent
目標(biāo)函數(shù) the objective
梯度驗(yàn)證方法 the derivative checking method
周韜(ztsailing@gmail.com)房维,葛燕儒(yrgehi@gmail.com),林鋒(xlfg@yeah.net)抬纸,余凱(kai.yu.cool@gmail.com)