抽象代數(shù)作為數(shù)學(xué)的一門學(xué)科沿癞,主要研究對(duì)象是代數(shù)結(jié)構(gòu)玖媚,比如群惑芭、環(huán)盅安、域面殖、模震缭、向量空間和代數(shù)峻贮。事實(shí)上席怪,對(duì)抽象代數(shù)的研究是應(yīng)數(shù)學(xué)更嚴(yán)格化的要求而發(fā)展起來的。對(duì)抽象代數(shù)的研究還使人們形成了對(duì)全部數(shù)學(xué)和自然科學(xué)的基礎(chǔ)性邏輯假設(shè)(的復(fù)雜性)的整體認(rèn)識(shí)纤控,現(xiàn)今挂捻,幾乎沒有那一個(gè)數(shù)學(xué)分支用不到代數(shù)學(xué)的結(jié)論。此外船万,隨著抽象代數(shù)的發(fā)展刻撒,代數(shù)學(xué)家們發(fā)現(xiàn):明顯不同的邏輯結(jié)構(gòu)通過類比可以得到一個(gè)很簡(jiǎn)練的由公理構(gòu)成的核心。這對(duì)深入研究代數(shù)的數(shù)學(xué)家是有益的耿导,并賦予他們更大的本領(lǐng)声怔。
20世紀(jì)初,抽象代數(shù)有時(shí)也稱為現(xiàn)代代數(shù)舱呻,近世代數(shù)醋火。
參見:http://zh.wikipedia.org/wiki/%E6%8A%BD%E8%B1%A1%E4%BB%A3%E6%95%B0
1. 代數(shù)結(jié)構(gòu):
一個(gè)代數(shù)結(jié)構(gòu)包含集合及符合某些公理的運(yùn)算或關(guān)系。
集U上定義二元運(yùn)算形成的系統(tǒng)稱為代數(shù)系統(tǒng)箱吕,如果對(duì)于任意a,b∈U,恒有(a·b)∈U芥驳。
二元運(yùn)算屬于數(shù)學(xué)運(yùn)算的一種。二元運(yùn)算需要三個(gè)元素:二元運(yùn)算符以及該運(yùn)算符作用的兩個(gè)變量茬高。
給定集合A兆旬,二元函數(shù)F: A×A→A稱為集合A上的二元運(yùn)算。
可以看出怎栽,“集合A上的二元運(yùn)算”這樣的提法暗示了該運(yùn)算在A上封閉丽猬。
二元運(yùn)算可推廣至多元運(yùn)算F,則相應(yīng)的封閉性要求則改為:對(duì)于任意a,b,c,d,……∈U,恒有F(a,b,c,d,……)∈U。
有的書上對(duì)封閉性未作要求熏瞄,并稱之為廣群脚祟。運(yùn)算f是一個(gè)從A×B→C的映射,若A=B=C,則稱運(yùn)算f是封閉的强饮。
以下是集中代數(shù)結(jié)構(gòu):
2. 群
在數(shù)學(xué)中由桌,群是一種代數(shù)結(jié)構(gòu),由一個(gè)集合以及一個(gè)二元運(yùn)算所組成。
一個(gè)群必須滿足一些被稱為“群公理”的條件
也就是:(1)封閉性(代數(shù)結(jié)構(gòu)就具備)沥寥、(2)結(jié)合律碍舍、(3)單位元和(4)逆元。
例如邑雅,整數(shù)配備上加法運(yùn)算就形成一個(gè)群片橡。(Z, +)是一個(gè)群。
群在數(shù)學(xué)內(nèi)外各個(gè)領(lǐng)域中是無處不在的淮野,這使得它們成為當(dāng)代數(shù)學(xué)的組成的中心原理捧书。
群的例子:
2.1 第一個(gè)例子:(Z, +):
最常見的群之一是整數(shù)集Z,它由以下數(shù)組成:
..., ?4, ?3, ?2, ?1, 0, 1, 2, 3, 4,?...
下列整數(shù)加法的性質(zhì)骤星,可以作為抽象的群公理的模型经瓷。
(1)封閉性:對(duì)于任何兩個(gè)整數(shù)a和b,它們的和a+b也是整數(shù)洞难。換句話說舆吮,在任何時(shí)候,把兩個(gè)整數(shù)相加都能得出整數(shù)的結(jié)果队贱。這個(gè)性質(zhì)叫做在加法下封閉色冀。
(2)結(jié)合律:對(duì)于任何整數(shù)a,b和c,(a+b) +c=a+(b+c)柱嫌。用話語來表達(dá)锋恬,先把a加到b,然后把它們的和加到c编丘,所得到的結(jié)果與把a加到b與c的和是相等的与学。這個(gè)性質(zhì)叫做結(jié)合律。
(3)單位元(既是左單位元又是右單位元):如果a是任何整數(shù)嘉抓,那么0 +a=a+ 0 =a索守。零叫做加法的單位元,因?yàn)榘阉拥饺魏握麛?shù)都得到相同的整數(shù)掌眠。
(4)逆元:對(duì)于任何整數(shù)a蕾盯,存在另一個(gè)整數(shù)b使得a+b=b+a= 0幕屹。整數(shù)b叫做整數(shù)a的逆元蓝丙,記為?a。
2.2 一般定義:
群是一個(gè)集合G望拖,連同一個(gè)運(yùn)算"·"渺尘,它結(jié)合任何兩個(gè)元素a和b而形成另一個(gè)元素,記為a·b说敏。符號(hào)"·"是對(duì)具體給出的運(yùn)算鸥跟,比如上面加法的一般的占位符。要具備成為群的資格,這個(gè)集合和運(yùn)算(G,·)必須滿足叫做群公理的四個(gè)要求:
(1).封閉性医咨。對(duì)于所有G中a,b枫匾,運(yùn)算a·b的結(jié)果也在G中。
(2).結(jié)合性拟淮。對(duì)于所有G中的a,b和c干茉,等式 (a·b)·c=a· (b·c)成立。
(3).單位元很泊。存在G中的一個(gè)元素e角虫,使得對(duì)于所有G中的元素a,等式e·a=a·e=a成立委造。
(4).逆元戳鹅。對(duì)于每個(gè)G中的a,存在G中的一個(gè)元素b使得a·b=b·a=e昏兆,這里的e是單位元枫虏。
進(jìn)行群運(yùn)算的次序是重要的。換句話說爬虱,把元素a與元素b結(jié)合模软,所得到的結(jié)果不一定與把元素b與元素a結(jié)合相同;等式
a·b=b·a
不一定恒成立饮潦。這個(gè)等式在整數(shù)于加法下的群中總是成立燃异,因?yàn)閷?duì)于任何兩個(gè)整數(shù)都有a+b=b+a(加法的交換律)。但是在一般的群中不總是成立继蜡。使等式a·b=b·a總是成立的群叫做阿貝爾群(以挪威數(shù)學(xué)家尼爾斯·阿貝爾命名)回俐。因此,整數(shù)加法群是阿貝爾群稀并,但一般群群不一定是仅颇。
2.3 阿貝爾群
阿貝爾群也稱為交換群或可交換群,它是滿足其元素的運(yùn)算不依賴于它們的次序(交換律公理)的群碘举。阿貝爾群推廣了整數(shù)集合的加法運(yùn)算忘瓦。阿貝爾群以挪威數(shù)學(xué)家尼爾斯·阿貝爾命名。
阿貝爾群是有著群運(yùn)算符合交換律性質(zhì)的群引颈,因此阿貝爾群也被稱為交換群耕皮。它由自身的集合G和二元運(yùn)算* 構(gòu)成。它除了滿足一般的群公理蝙场,即運(yùn)算的結(jié)合律凌停、G有單位元、所有G的元素都有逆元之外售滤,還滿足交換律公理:
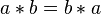
而群運(yùn)算不滿足交換律的群被稱為“非阿貝爾群”罚拟,或“非交換群”台诗。
2.4 環(huán)
環(huán)(Ring)的定義類似于可交換群,只不過在原來“+”的基礎(chǔ)上又增添另一種運(yùn)算“·”(注意我們這里所說的 + 與 · 一般不是我們所熟知的四則運(yùn)算加法和乘法)赐俗。在抽象代數(shù)中拉队,研究環(huán)的分支為環(huán)論。
集合R和定義于其上的二元運(yùn)算 + 和·阻逮,(R, +, ·)構(gòu)成一個(gè)環(huán)氏仗,若它們滿足:
(1) (R, +)形成一個(gè)交換群,也就是一個(gè)阿貝爾群夺鲜。其單位元稱為零元皆尔,記作‘0’。即:
? ? ? ? ? ①(R, +)是封閉的
? ? ? ? ? ②(a + b) = (b + a)
? ? ? ? ? ③(a + b) + c = a + (b + c)
? ? ? ? ? ④0 + a = a + 0 = a
? ? ? ? ? ⑤?a ?(?a) 滿足 a + ?a = ?a + a = 0
(2) (R, ·)形成一個(gè)半群币励,即:
????????? ①(a·b)·c = a·(b·c)
? ? ? ? ? ②(R, ·)是封閉的
(3)乘法關(guān)于加法滿足分配律:
????????? ①a·(b + c) = (a·b) + (a·c)
????????? ②(a + b)·c = (a·c) + (b·c)
其中慷蠕,乘法運(yùn)算符·常被省略,所以 a·b 可簡(jiǎn)寫為 ab食呻。 此外流炕,乘法是比加法優(yōu)先的運(yùn)算,所以 a + bc 其實(shí)是 a + (b·c)仅胞。
補(bǔ):交換環(huán)(commutative ring)是乘法運(yùn)算滿足交換律的環(huán)
環(huán)是一個(gè)集合R帶有兩個(gè)二元運(yùn)算每辟,即將環(huán)中的任意兩個(gè)元素變?yōu)榈谌齻€(gè)的運(yùn)算。他們稱為加法與乘法干旧,通常記作 + 與 ? 渠欺,例如a+b與a?b。為了形成一個(gè)群這兩個(gè)運(yùn)算需滿足一些性質(zhì):環(huán)在加法下是一個(gè)阿貝爾群椎眯,在乘法下為一個(gè)幺半群挠将,使得乘法對(duì)加法有分配律,即a? (b+c) = (a?b) + (a?c)编整。關(guān)于加法與乘法的單位元素分別記作 0 和 1舔稀。
另外如果乘法也是交換的,即
a?b=b?a掌测,
環(huán)R稱為交換的内贮。
一個(gè)重要的例子,在某種意義下是最關(guān)鍵的汞斧,是帶有加法與乘法兩個(gè)運(yùn)算的整數(shù)環(huán)Z夜郁。因?yàn)檎麛?shù)乘法是一個(gè)交換運(yùn)算,這是一個(gè)交換環(huán)断箫。通常記作Z拂酣,是德語詞Zahlen(數(shù))的縮寫秋冰。
2.5 域
域是一種交換環(huán)(F, +, *)仲义,當(dāng)中加法單位元(0)不等于乘法單位元(1),且所有非零元素有乘法逆元。
一個(gè)域是每個(gè)非零元素a是可逆的交換環(huán)埃撵,即有一個(gè)乘法逆b使得a?b= 1赵颅。從而,由定義知任何域是一個(gè)交換環(huán)暂刘。有理數(shù)饺谬、實(shí)數(shù)、復(fù)數(shù)都是域谣拣。
2×2 的矩陣不是交換的募寨,因?yàn)?a target="_blank" rel="nofollow">矩陣乘法不滿足交換律。
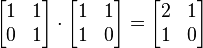
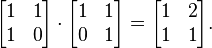
但是拔鹰,能被相同的相似變換對(duì)角化的矩陣形成一個(gè)交換環(huán)。一個(gè)例子是關(guān)于一個(gè)固定節(jié)點(diǎn)集合差商的矩陣集合贵涵。