二叉堆的定義
二叉堆是完全二叉樹或者是近似完全二叉樹掏导。
二叉堆滿足二個(gè)特性:
- 父結(jié)點(diǎn)的鍵值總是大于或等于(小于或等于)任何一個(gè)子節(jié)點(diǎn)的鍵值。
- 每個(gè)結(jié)點(diǎn)的左子樹和右子樹都是一個(gè)二叉堆(都是最大堆或最小堆)。
當(dāng)父結(jié)點(diǎn)的鍵值總是大于或等于任何一個(gè)子節(jié)點(diǎn)的鍵值時(shí)為最大堆密幔。當(dāng)父結(jié)點(diǎn)的鍵值總是小于或等于任何一個(gè)子節(jié)點(diǎn)的鍵值時(shí)為最小堆姆另。下圖展示一個(gè)最小堆:
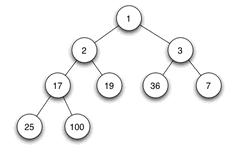
由于其它幾種堆(二項(xiàng)式堆,斐波納契堆等)用的較少孩哑,一般將二叉堆就簡稱為堆栓霜。
堆的存儲(chǔ)
一般都用數(shù)組來表示堆,i結(jié)點(diǎn)的父結(jié)點(diǎn)下標(biāo)就為(i – 1)/2横蜒。它的左右子結(jié)點(diǎn)下標(biāo)分別為2 * i + 1和2 * i + 2胳蛮。如第0個(gè)結(jié)點(diǎn)左右子結(jié)點(diǎn)下標(biāo)分別為1和2。

堆的操作——插入刪除
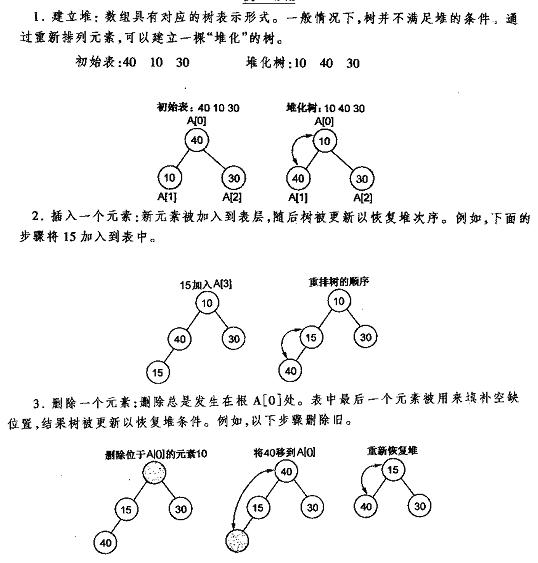
堆的插入
每次插入都是將新數(shù)據(jù)放在數(shù)組最后丛晌〗龃叮可以發(fā)現(xiàn)從這個(gè)新數(shù)據(jù)的父結(jié)點(diǎn)到根結(jié)點(diǎn)必然為一個(gè)有序的數(shù)列,現(xiàn)在的任務(wù)是將這個(gè)新數(shù)據(jù)插入到這個(gè)有序數(shù)據(jù)中——這就類似于直接插入排序中將一個(gè)數(shù)據(jù)并入到有序區(qū)間中.
// 新加入i結(jié)點(diǎn) 其父結(jié)點(diǎn)為(i - 1) / 2
void MinHeapFixup(int a[], int i)
{
int j, temp;
temp = a[i];
j = (i - 1) / 2; //父結(jié)點(diǎn)
while (j >= 0 && i != 0)
{
if (a[j] <= temp)
break;
a[i] = a[j]; //把較大的子結(jié)點(diǎn)往下移動(dòng),替換它的子結(jié)點(diǎn)
i = j;
j = (i - 1) / 2;
}
a[i] = temp;
}
//在最小堆中加入新的數(shù)據(jù)nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
a[n] = nNum;
MinHeapFixup(a, n);
}
堆的刪除
按定義澎蛛,堆中每次都只能刪除第0個(gè)數(shù)據(jù)抚垄。為了便于重建堆,實(shí)際的操作是將最后一個(gè)數(shù)據(jù)的值賦給根結(jié)點(diǎn),然后再從根結(jié)點(diǎn)開始進(jìn)行一次從上向下的調(diào)整呆馁。調(diào)整時(shí)先在左右兒子結(jié)點(diǎn)中找最小的桐经,如果父結(jié)點(diǎn)比這個(gè)最小的子結(jié)點(diǎn)還小說明不需要調(diào)整了,反之將父結(jié)點(diǎn)和它交換后再考慮后面的結(jié)點(diǎn)浙滤。相當(dāng)于從根結(jié)點(diǎn)將一個(gè)數(shù)據(jù)的“下沉”過程阴挣。下面給出代碼:
// 從i節(jié)點(diǎn)開始調(diào)整,n為節(jié)點(diǎn)總數(shù) 從0開始計(jì)算 i節(jié)點(diǎn)的子節(jié)點(diǎn)為 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把較小的子結(jié)點(diǎn)往上移動(dòng),替換它的父結(jié)點(diǎn)
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//在最小堆中刪除數(shù)
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}
堆化數(shù)組
有了堆的插入和刪除后,再考慮下如何對(duì)一個(gè)數(shù)據(jù)進(jìn)行堆化操作纺腊。要一個(gè)一個(gè)的從數(shù)組中取出數(shù)據(jù)來建立堆吧畔咧,不用!先看一個(gè)數(shù)組揖膜,如下圖:
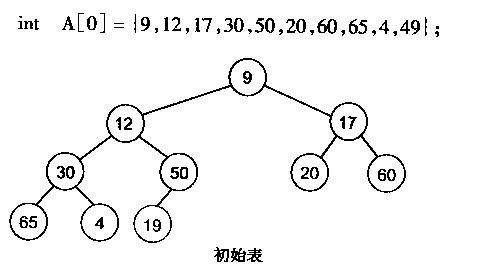
很明顯誓沸,對(duì)葉子結(jié)點(diǎn)來說,可以認(rèn)為它已經(jīng)是一個(gè)合法的堆了即20壹粟,60拜隧, 65, 4煮寡, 49都分別是一個(gè)合法的堆虹蓄。只要從A[4]=50開始向下調(diào)整就可以了。然后再取A[3]=30幸撕,A[2] = 17薇组,A[1] = 12,A[0] = 9分別作一次向下調(diào)整操作就可以了坐儿。下圖展示了這些步驟:
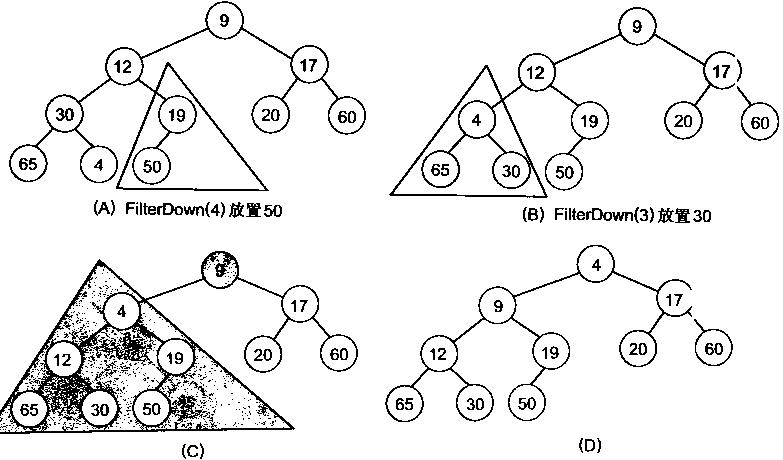
寫出堆化數(shù)組的代碼:
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
MinHeapFixdown(a, i, n);
}
堆排序
首先可以看到堆建好之后堆中第0個(gè)數(shù)據(jù)是堆中最小的數(shù)據(jù)律胀。取出這個(gè)數(shù)據(jù)再執(zhí)行下堆的刪除操作。這樣堆中第0個(gè)數(shù)據(jù)又是堆中最小的數(shù)據(jù)貌矿,重復(fù)上述步驟直至堆中只有一個(gè)數(shù)據(jù)時(shí)就直接取出這個(gè)數(shù)據(jù)炭菌。
由于堆也是用數(shù)組模擬的,故堆化數(shù)組后逛漫,第一次將A[0]與A[n - 1]交換黑低,再對(duì)A[0…n-2]重新恢復(fù)堆。第二次將A[0]與A[n – 2]交換酌毡,再對(duì)A[0…n - 3]重新恢復(fù)堆克握,重復(fù)這樣的操作直到A[0]與A[1]交換。由于每次都是將最小的數(shù)據(jù)并入到后面的有序區(qū)間枷踏,故操作完成后整個(gè)數(shù)組就有序了菩暗。有點(diǎn)類似于直接選擇排序
void MinheapsortTodescendarray(int a[], int n)
{
for (int i = n - 1; i >= 1; i--)
{
Swap(a[i], a[0]);
MinHeapFixdown(a, 0, i);
}
}
注意使用最小堆排序后是遞減數(shù)組,要得到遞增數(shù)組旭蠕,可以使用最大堆停团。
由于每次重新恢復(fù)堆的時(shí)間復(fù)雜度為O(logN)旷坦,共N - 1次重新恢復(fù)堆操作,再加上前面建立堆時(shí)N / 2次向下調(diào)整佑稠,每次調(diào)整時(shí)間復(fù)雜度也為O(logN)秒梅。二次操作時(shí)間相加還是O(N * logN)。故堆排序的時(shí)間復(fù)雜度為O(N * logN)讶坯。
轉(zhuǎn)載請(qǐng)標(biāo)明出處番电,原文地址:http://blog.csdn.net/morewindows/article/details/6709644