正則化是一種回歸的形式裕寨,它將系數(shù)估計(jì)(coefficient estimate)朝零的方向進(jìn)行約束浩蓉、調(diào)整或縮小。也就是說(shuō)宾袜,正則化可以在學(xué)習(xí)過(guò)程中降低模型復(fù)雜度和不穩(wěn)定程度捻艳,從而避免過(guò)擬合的危險(xiǎn)。
一庆猫、數(shù)學(xué)基礎(chǔ)
1. 范數(shù)
范數(shù)是衡量某個(gè)向量空間(或矩陣)中的每個(gè)向量以長(zhǎng)度或大小认轨。范數(shù)的一般化定義:對(duì)實(shí)數(shù)p>=1, 范數(shù)定義如下:
-
L1范數(shù)
當(dāng)p=1時(shí)月培,是L1范數(shù)嘁字,其表示某個(gè)向量中所有元素絕對(duì)值的和。 -
L2范數(shù)
當(dāng)p=2時(shí)杉畜,是L2范數(shù)纪蜒, 表示某個(gè)向量中所有元素平方和再開根, 也就是歐幾里得距離公式此叠。
2. 拉普拉斯分布
如果隨機(jī)變量的概率密度函數(shù)分布為:


3. 高斯分布
又叫正態(tài)分布显沈,若隨機(jī)變量X服從一個(gè)數(shù)學(xué)期望為μ、標(biāo)準(zhǔn)方差為σ2的高斯分布析校,記為:X~N(μ,σ2)构罗,其概率密度函數(shù)為:

還有涉及極大似然估計(jì)、概率論相關(guān)的先驗(yàn)和后驗(yàn)相關(guān)概率吊奢, 為了控制篇幅盖彭, 本文就不詳細(xì)介紹, wiki百科和百度百科都講得很清楚页滚。
二召边、正則化解決過(guò)擬合問(wèn)題
正則化通過(guò)降低模型的復(fù)雜性, 達(dá)到避免過(guò)擬合的問(wèn)題裹驰。 正則化是如何解決過(guò)擬合的問(wèn)題的呢隧熙?從網(wǎng)上找了很多相關(guān)文章, 下面列舉兩個(gè)主流的解釋方式幻林。


如果發(fā)生過(guò)擬合, 參數(shù)θ一般是比較大的值鼠次, 加入懲罰項(xiàng)后, 只要控制λ的大小,當(dāng)λ很大時(shí)腥寇,θ1到θn就會(huì)很小成翩,即達(dá)到了約束數(shù)量龐大的特征的目的。
原因二:從貝葉斯的角度來(lái)分析赦役, 正則化是為模型參數(shù)估計(jì)增加一個(gè)先驗(yàn)知識(shí)麻敌,先驗(yàn)知識(shí)會(huì)引導(dǎo)損失函數(shù)最小值過(guò)程朝著約束方向迭代。 L1正則是拉普拉斯先驗(yàn)掂摔,L2是高斯先驗(yàn)术羔。整個(gè)最優(yōu)化問(wèn)題可以看做是一個(gè)最大后驗(yàn)估計(jì),其中正則化項(xiàng)對(duì)應(yīng)后驗(yàn)估計(jì)中的先驗(yàn)信息乙漓,損失函數(shù)對(duì)應(yīng)后驗(yàn)估計(jì)中的似然函數(shù)级历,兩者的乘積即對(duì)應(yīng)貝葉斯最大后驗(yàn)估計(jì)。
給定訓(xùn)練數(shù)據(jù), 貝葉斯方法通過(guò)最大化后驗(yàn)概率估計(jì)參數(shù)θ:

下面我們從最大后驗(yàn)估計(jì)(MAP)的方式寥殖, 推導(dǎo)下加入L1和L2懲罰項(xiàng)的Lasso和嶺回歸的公式。
首先我們看下最小二乘公式的推導(dǎo)(公式推導(dǎo)截圖來(lái)自知乎大神)

-
假設(shè)1: w參數(shù)向量服從高斯分布
以下為貝葉斯最大后驗(yàn)估計(jì)推導(dǎo):
最終的公式就是嶺回歸計(jì)算公式。與上面最大似然估計(jì)推導(dǎo)出的最小二乘相比同诫,最大后驗(yàn)估計(jì)就是在最大似然估計(jì)公式乘以高斯先驗(yàn)粤策, 這里就理解前面L2正則就是加入高斯先驗(yàn)知識(shí)。 -
假設(shè)2: w參數(shù)服從拉普拉斯分布
以下為貝葉斯最大后驗(yàn)估計(jì)推導(dǎo):
最終的公式就是Lasso計(jì)算公式误窖。與上面最大似然估計(jì)推導(dǎo)出的最小二乘相比叮盘,最大后驗(yàn)估計(jì)就是在最大似然估計(jì)公式乘以拉普拉斯先驗(yàn), 這里就理解前面L1正則就是加入拉普拉斯先驗(yàn)知識(shí)贩猎。
L1和L2正則化的比較
為了幫助理解熊户,我們來(lái)看一個(gè)直觀的例子:假定x僅有兩個(gè)屬性,于是無(wú)論嶺回歸還是Lasso接觸的w都只有兩個(gè)分量吭服,即w1,w2嚷堡,我們將其作為兩個(gè)坐標(biāo)軸,然后在圖中繪制出兩個(gè)式子的第一項(xiàng)的”等值線”艇棕,即在(w1,w2)空間中平方誤差項(xiàng)取值相同的點(diǎn)的連線蝌戒。再分別繪制出L1范數(shù)和L2范數(shù)的等值線,即在(w1,w2)空間中L1范數(shù)取值相同的點(diǎn)的連線沼琉,以及L2范數(shù)取值相同的點(diǎn)的連線(如下圖所示)北苟。
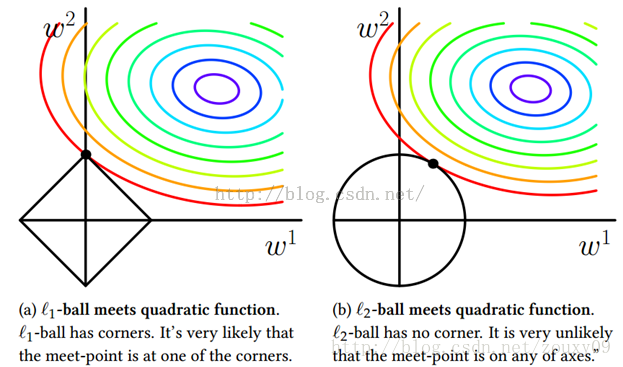
嶺回歸與Lasso的解都要在平方誤差項(xiàng)與正則化項(xiàng)之間折中,即出現(xiàn)在圖中平方誤差項(xiàng)等值線與正則化項(xiàng)等值線相交處打瘪。而由上圖可以看出友鼻,采用L1范數(shù)時(shí)平方誤差項(xiàng)等值線與正則化項(xiàng)等值線的交點(diǎn)常出現(xiàn)在坐標(biāo)軸上傻昙,即w1或w2為0,而在采用L2范數(shù)時(shí)彩扔,兩者的交點(diǎn)常出現(xiàn)在某個(gè)象限中妆档,即w1或w2均非0。
這說(shuō)明了嶺回歸的一個(gè)明顯缺點(diǎn):模型的可解釋性虫碉。它將把不重要的預(yù)測(cè)因子的系數(shù)縮小到趨近于 0贾惦,但永不達(dá)到 0。也就是說(shuō)敦捧,最終的模型會(huì)包含所有的預(yù)測(cè)因子须板。但是,在 Lasso 中兢卵,如果將調(diào)整因子 λ 調(diào)整得足夠大习瑰,L1 范數(shù)懲罰可以迫使一些系數(shù)估計(jì)值完全等于 0。因此济蝉,Lasso 可以進(jìn)行變量選擇杰刽,產(chǎn)生稀疏模型。注意到w取得稀疏解意味著初始的d個(gè)特征中僅有對(duì)應(yīng)著w的非零分量的特征才會(huì)出現(xiàn)在最終模型中王滤,于是求解L1范數(shù)正則化的結(jié)果時(shí)得到了僅采用一部分初始特征的模型贺嫂;換言之,基于L1正則化的學(xué)習(xí)方法就是一種嵌入式特征選擇方法雁乡,其特征選擇過(guò)程和學(xué)習(xí)器訓(xùn)練過(guò)程融為一體第喳,同時(shí)完成。
總結(jié)
- L2 regularizer :使得模型的解偏向于范數(shù)較小的 W踱稍,通過(guò)限制 W 范數(shù)的大小實(shí)現(xiàn)了對(duì)模型空間的限制曲饱,從而在一定程度上避免了 overfitting 。不過(guò) ridge regression 并不具有產(chǎn)生稀疏解的能力珠月,得到的系數(shù)仍然需要數(shù)據(jù)中的所有特征才能計(jì)算預(yù)測(cè)結(jié)果扩淀,從計(jì)算量上來(lái)說(shuō)并沒有得到改觀。
- L1 regularizer :它的優(yōu)良性質(zhì)是能產(chǎn)生稀疏性啤挎,導(dǎo)致 W 中許多項(xiàng)變成零驻谆。 稀疏的解除了計(jì)算量上的好處之外,更重要的是更具有“可解釋性”庆聘。

