我們很早就學(xué)過喘垂,圓的面積計算公式:

但是以前從沒想過他是怎么推導(dǎo)來的甜刻,今天突發(fā)奇想,用微積分推導(dǎo)了一下正勒,然后上網(wǎng)看了下高手們的推導(dǎo)得院,真的是各種方法無奇不有啊,于是就有了寫這篇文章的沖動章贞,總結(jié)下各種計算圓面積的方法祥绞。
不需要常數(shù)π的方法
計算圓的面積中有一個重要常數(shù)π,現(xiàn)在假設(shè)我們不知道π的值鸭限,該怎么計算圓的面積呢蜕径?
蒙特卡羅方法(或飛鏢法)
不知道常數(shù)π的值,也就沒法直接求出圓的周長和面積败京,很好想到的一個方法就是:將圓鑲嵌在一個正方形中兜喻,然后求出圓占這個正方形面積的百分比:

你可以胡亂朝這個區(qū)域投擲飛鏢,當(dāng)飛鏢數(shù)量足夠大赡麦,并假設(shè)飛鏢投到這個區(qū)域任意位置的概率是一樣的朴皆,那么你最后就可以通過飛鏢數(shù)量求出圓占整個正方形面積的比,設(shè)圓的半徑為r泛粹,正方形面積為:

由知道了比值遂铡,自然就可以算出圓的面積
需要常數(shù)π的方法
常數(shù)π是個重要的常數(shù),它表示圓的周長C和圓的直徑d之比:

如果要用公式:

計算圓的面積晶姊,當(dāng)然需要知道π的值扒接。
知道了π的定義,最簡單的辦法就是滾粗法:

操作起來就是:
先用繩子圍繞標(biāo)準(zhǔn)圓一周们衙,然后測量繩子長度:

接著找準(zhǔn)圓心钾怔,然后用尺子測出圓的直徑:

這兩的比值就是常數(shù)π了。當(dāng)然為了更好的精確度砍艾,可以采用多次測量取平均值的方法蒂教。
其實上面講到的蒙特卡洛方法也可以用來計算常數(shù)π,只需將圓的半徑設(shè)為1就好脆荷。
還有一種經(jīng)典的蒙特卡洛方法,叫做蒲風(fēng)投針實驗:
設(shè)針的長度是l,平行線之間的距離為t,x為針的中心和最近的平行線的距離,θ為針和線之間的銳角蜓谋。

可以推導(dǎo):

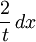
而
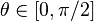
的概率密度函數(shù)為:

x和θ兩個隨機變數(shù)互相獨立梦皮,因此兩者結(jié)合的概率密度函數(shù)只是兩者的積:

針和線相交時:

求上式的積分,得到針和線相交的概率:

即拋n針桃焕,其中有h針和線相交的概率為:
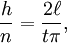
由此可以得到π:

具體操作時剑肯,我們可以取t=2l,然后投擲n針观堂,除以針和線相交的次數(shù)h让网,就得到π:

當(dāng)然還有更多計算π的方法,像數(shù)列求極限等师痕,感興趣的請參考這里
好了溃睹,解決了常數(shù)π,下面回到正題胰坟,如何計算圓的面積因篇?
剪紙法
剪紙法的思想就是化整為零,再重新拼接笔横。

將一個圓剪成很多小的扇形竞滓,然后再將其拼成如上圖的一個矩形,由于圓的周長是2πr,藍色和黃色各占一半吹缔,所以拼成的長方形的長約為π*r,而長方形的寬約為圓的半徑r商佑,所以圓的面積等于長方形的面積:

變形法
其實這個方法和上個方法基本思想是一樣的:圓的面積我們不知道,那能不能把圓轉(zhuǎn)換成我們熟悉的形狀呢厢塘?比如三角形:

三角形的面積公式我們知道莉御,那與它等價的圓的面積自然也就能計算了:

微積分法
大學(xué)里學(xué)了微積分,用微積分來計算圓的面積俗冻,那不是拿著刀俎礁叔,魚肉隨便切嗎。不過雖然都是用微積分迄薄,出發(fā)思想不一樣琅关,解法也不一樣。
洋蔥法
使用微積分讥蔽,我們將圓象洋蔥一樣分為薄圓環(huán)涣易,遞增地求出面積。

對“洋蔥”冶伞,以 t 為半徑的無窮薄圓環(huán)新症,貢獻的面積是 2πt dt,周長的長度乘以其無窮小寬度响禽。這樣對半徑為 r 的圓給出了一個初等積分:

極坐標(biāo)法
極坐標(biāo)也是一種變換的方法徒爹,就像傅里葉變換一樣荚醒,極坐標(biāo)變換將直角坐標(biāo)系下看似復(fù)雜的東西變成極坐標(biāo)系下極其簡單的東西,就像在直角坐標(biāo)系下的一個圓環(huán)隆嗅,在極坐標(biāo)系下卻是長方形:

唯一要注意的是界阁,直角坐標(biāo)系下的面積微元為:dxdy,而極坐標(biāo)下卻是:tdtdθ,不懂可以參考這里
使用極坐標(biāo)下的二重積分胖喳,積分函數(shù)為f(x)=1, 積分區(qū)域為圓C泡躯,則:

分割傘形法
類似于洋蔥法,我們也可以把圓分割為一系列小的傘形區(qū)域丽焊,則每個區(qū)域的面積近似為二分之一的弧長(rdθ)乘以半徑r:

然后將dθ從0到2π積分较剃,就可以計算出圓的面積:

半圓法
我們知道,圓的方程為:

由此可得技健,當(dāng)y>0時写穴,半圓的方程為:

對函數(shù)y從-r到r積分,由積分的定義知凫乖,積分的結(jié)果為二分之一圓的面積确垫。
要計算:

我們先假設(shè):

則:


那么:

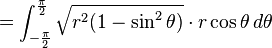
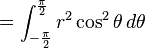



當(dāng)然,你可以通過mathmatica,直接得到結(jié)果:

總結(jié)
以上的一些方法帽芽,歸根結(jié)底就兩類思想:要么是轉(zhuǎn)化的思想删掀,將圓轉(zhuǎn)化為熟悉的圖形計算,要么是微積分的思想导街,把圓細(xì)分為微單元披泪,然后再將這些微單元相加。一個簡單的圓面積公式搬瑰,都有這么多的解法款票,數(shù)學(xué)的魅力就在這里。
參考文獻
wikipedia
圓的面積
calculus proof for the area of a circle
計算圓周率-Pi
布豐投針問題
圓周率