文章轉自:泊松分布和指數(shù)分布:10分鐘教程 - 阮一峰的網絡日志
http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html
以及 ??如何理解泊松分布和泊松過程-czxttkl-搜狐博客!!!
http://maider.blog.sohu.com/304621504.html
以及? 知乎泊松分布的現(xiàn)實意義是什么宇姚,為什么現(xiàn)實生活多數(shù)服從于泊松分布茬腿?劉一鳴的回答
?https://www.zhihu.com/question/26441147/answer/32786384
泊松分布和指數(shù)分布:10分鐘教程
作者:阮一峰
日期:2015年6月10日
大學時,我一直覺得統(tǒng)計學很難,還差點掛科。
工作以后才發(fā)現(xiàn),難的不是統(tǒng)計學庄蹋,而是我們的教材寫得不好瞬内。比起高等數(shù)學,統(tǒng)計概念其實容易理解多了限书。
我舉一個例子虫蝶,什么是泊松分布和指數(shù)分布?恐怕大多數(shù)人都說不清楚倦西。
我可以在10分鐘內能真,讓你毫不費力地理解這兩個概念。
一扰柠、泊松分布
日常生活中粉铐,大量事件是有固定頻率的。
某醫(yī)院平均每小時出生3個嬰兒
某公司平均每10分鐘接到1個電話
某超市平均每天銷售4包xx牌奶粉
某網站平均每分鐘有2次訪問
它們的特點就是卤档,我們可以預估這些事件的總數(shù)蝙泼,但是沒法知道具體的發(fā)生時間。已知平均每小時出生3個嬰兒劝枣,請問下一個小時汤踏,會出生幾個?

有可能一下子出生6個舔腾,也有可能一個都不出生溪胶。這是我們沒法知道的。
泊松分布就是描述某段時間內稳诚,事件具體的發(fā)生概率哗脖。
上面就是泊松分布的公式。等號的左邊采桃,P 表示概率懒熙,N表示某種函數(shù)關系,t 表示時間普办,n 表示數(shù)量工扎,1小時內出生3個嬰兒的概率,就表示為 P(N(1) = 3) 衔蹲。等號的右邊肢娘,λ 表示事件的頻率。
接下來兩個小時舆驶,一個嬰兒都不出生的概率是0.25%橱健,基本不可能發(fā)生。
接下來一個小時沙廉,至少出生兩個嬰兒的概率是80%拘荡。
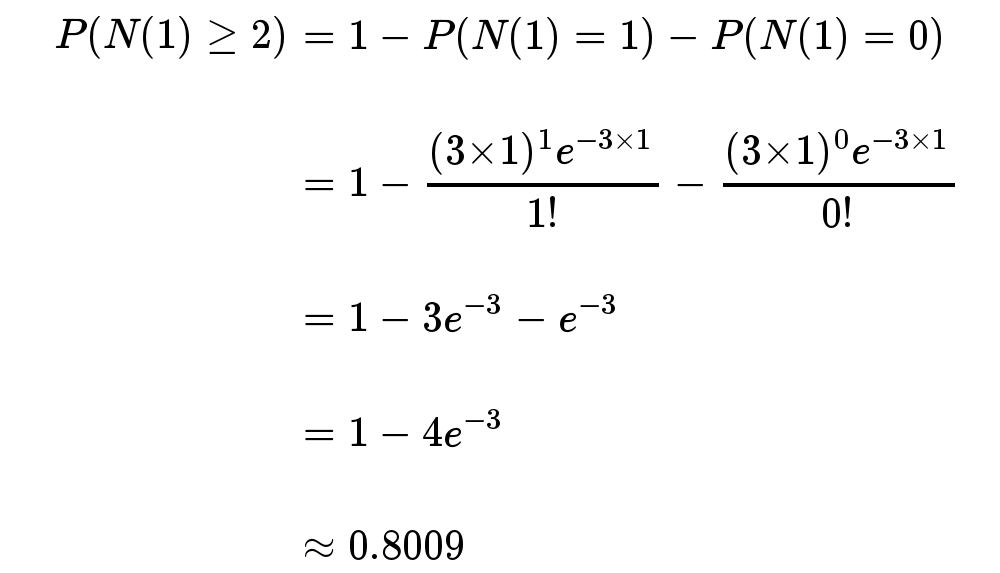
泊松分布的圖形大概是下面的樣子。
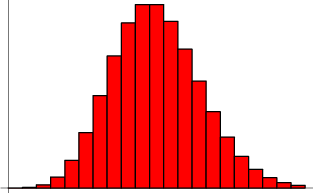
可以看到撬陵,在頻率附近珊皿,事件的發(fā)生概率最高网缝,然后向兩邊對稱下降,即變得越大和越小都不太可能蟋定。每小時出生3個嬰兒粉臊,這是最可能的結果,出生得越多或越少驶兜,就越不可能扼仲。
二、指數(shù)分布
指數(shù)分布是事件的時間間隔的概率抄淑。下面這些都屬于指數(shù)分布屠凶。
嬰兒出生的時間間隔
來電的時間間隔
奶粉銷售的時間間隔
網站訪問的時間間隔
指數(shù)分布的公式可以從泊松分布推斷出來。如果下一個嬰兒要間隔時間 t 蝇狼,就等同于 t 之內沒有任何嬰兒出生阅畴。

反過來倡怎,事件在時間 t 之內發(fā)生的概率迅耘,就是1減去上面的值。

接下來15分鐘监署,會有嬰兒出生的概率是52.76%颤专。

接下來的15分鐘到30分鐘,會有嬰兒出生的概率是24.92%钠乏。

指數(shù)分布的圖形大概是下面的樣子栖秕。

可以看到,隨著間隔時間變長晓避,事件的發(fā)生概率急劇下降簇捍,呈指數(shù)式衰減。想一想俏拱,如果每小時平均出生3個嬰兒暑塑,上面已經算過了,下一個嬰兒間隔2小時才出生的概率是0.25%锅必,那么間隔3小時事格、間隔4小時的概率,是不是更接近于0搞隐?
三驹愚、總結

一句話總結:泊松分布是單位時間內獨立事件發(fā)生次數(shù)的概率分布,指數(shù)分布是獨立事件的時間間隔的概率分布劣纲。
請注意是"獨立事件"逢捺,泊松分布和指數(shù)分布的前提是,事件之間不能有關聯(lián)癞季,否則就不能運用上面的公式劫瞳。
[說明] 本文受到nbviewer 文檔的啟發(fā)棠耕。
(正文完)
================================================
背景
阮一峰的博客講到了如何理解泊松分布:
http://www.ruanyifeng.com/blog/2013/01/poisson_distribution.html
本文根據其文繼續(xù)講講。
泊松分布的由來
泊松分布由二項分布演進而來柠新。二項分布十分好理解窍荧,給你n次機會拋硬幣,硬幣正面向上的概率為p恨憎,問在這n次機會中有k次(k<=n)硬幣朝上的概率為多少蕊退?
在這n次拋硬幣中,硬幣朝上的次數(shù)的期望有多少憔恳?
如果現(xiàn)在我能根據n的大小來控制p瓤荔,從而控制這個期望,即無論n為多大钥组,硬幣朝上的次數(shù)的期望不變(恒為lambda):
那么當n趨于無窮的時候输硝,P(K_heads)將趨于泊松分布,即:
推到過程見(Introduction To Probability p307:https://www.dropbox.com/s/mrss8wg5yvmf7kw/Introduction%20to%20Probability.pdf)
所以程梦,實驗結果滿足泊松分布的實驗即為泊松過程点把。泊松過程把離散的伯努利過程變得連續(xù)化了:原來是拋n次硬幣,現(xiàn)在變成了無窮多次拋硬幣屿附;原來某次拋硬幣得到正面的概率是p郎逃,而現(xiàn)在p無限接近于0(p=lambda/n),即:非常難拋出正面朝上的硬幣挺份;但是n次實驗中硬幣朝上的次數(shù)的期望不變褒翰,即lambda恒定。在泊松過程中匀泊,我們把拋出硬幣正面這樣的事件叫做到達(Arrival)优训。把單位時間內到達的數(shù)量,叫做到達率(Arrival Rate)各聘。
故揣非,泊松過程需要滿足以下三個性質:
1. 在任意單位時間長度內,到達率是穩(wěn)定的伦吠。對應于無窮次拋硬幣的例子妆兑,我們相當于把一個單位時間分割成了無窮次拋硬幣的實驗,每次實驗產生正面的概率都是一樣的(為lambda/n)毛仪,而在這無窮個拋硬幣實驗之后(即一個單位時間之后)我們期望能拋出lambda個正面的硬幣搁嗓。這個性質類比于在有限次拋硬幣(二次分布)的例子中保證了每次擲出硬幣為正面的概率都為p。
2. 未來的實驗結果與過去的實驗結果無關箱靴。對應于無窮次拋硬幣的例子腺逛,之前不管拋出了多少個正面和反面的硬幣,都不會影響之后硬幣出現(xiàn)的結果衡怀。
3. 在極小的一段時間內棍矛,有1次到達的概率非常小安疗,沒有到達的概率非常大。對應于無窮次拋硬幣的例子够委,我們發(fā)現(xiàn)硬幣朝上的概率p=lambda/n趨向于0荐类。
判斷一個過程是否為泊松過程
現(xiàn)在我們來講講阮一峰所舉的槍擊案的例子。這個例子給你了美國30年來每年的槍擊案發(fā)生數(shù)目茁帽,需要解決的問題是能否從每年發(fā)生槍擊案的數(shù)目判斷美國槍擊犯罪是否惡化玉罐。假設美國槍擊案犯罪沒有惡化,而是非常穩(wěn)定潘拨,我們可以假設:槍擊案的發(fā)生為泊松過程吊输,每年平均發(fā)生槍擊案的數(shù)目恒定(性質1),各個年份之間發(fā)生槍擊案的數(shù)目不互相影響(性質2)铁追,任一時刻發(fā)生槍擊案的概率很屑韭臁(性質3),所以每年發(fā)生槍擊案的數(shù)目服從泊松分布琅束。
如何證明我們的假設是對的呢扭屁?如果槍擊案的發(fā)生為泊松過程,我們可以從數(shù)據中算出到達率lambda(年平均發(fā)生槍擊案數(shù)目)為2狰闪。因為在我們的假設下每年發(fā)生槍擊案的數(shù)目服從泊松分布疯搅,那么一年內發(fā)生0起槍擊案的概率為
一年內發(fā)生1起槍擊案的概率為
依此類推濒生,那么我們可以得到一張我們假設出的年槍擊案數(shù)目分布和實際槍擊案發(fā)生數(shù)目的對照表:
以及分布圖:
再由一些統(tǒng)計學的計算方法(非本文重點埋泵,細節(jié)參見阮一峰原文),計算出我們假設的值與實際觀測的值是否接近。如果接近罪治,則說明我們的假設-槍擊案發(fā)生為泊松過程-是正確的丽声。
The Random Incidence Paradox
我們先來看看一個經典的Paradox:
上面的例子告訴了我們,假設一個事件的平均到達時間為T觉义,你作為觀察者多次介入該事件雁社,并記錄連續(xù)兩個到達間隔的時間,你記錄得到的平均到達時間會比T更長晒骇。你現(xiàn)在是在抽樣“前后兩次到達的間隔時間”霉撵,你介入該事件并開始記錄是等概的,但你并不是等概地抽取不同到達間隔時間的樣本:你更加有可能碰到兩次到達間隔時間較長的情況洪囤,導致你最后的結果存在了BIAS徒坡。
那么現(xiàn)在也就更好理解下面的一個問題:
如果在一種BUS到達station為泊松過程,其到達率為lambda瘤缩,即平均等待時間為1/lambda喇完。你作為觀察者在任意時間進入station,并多次記錄前后到達時間的間隔(這里意為剥啤,你進入station時就可以立馬知道前一次到達的時間锦溪,然后開始等待直到下一次到達并記錄)不脯。求問你記錄的平均到達間隔時間為多少?
答案肯定是大于1/lambda的刻诊。假設你到達的時刻為t*防楷,前一到達時刻為U,后一將要到達時刻為L则涯,那么U至t*可以看做一段泊松過程域帐,t*到L也可以看做一段泊松過程,所以你記錄的平均到達間隔時間應該是兩個泊松過程相加后的平均等待時間是整。多個泊松過程相加得到的是愛爾蘭(Erlang)過程肖揣,期望為k/lambda。所以本題最后的答案是2/lambda浮入。
知乎劉一鳴的回答:
鏈接:https://www.zhihu.com/question/26441147/answer/32786384
在一個時間段內事件平均發(fā)生的次數(shù)服從泊松分布,這個次數(shù)在泊松分布中用lambda表示事秀。這個lambda在指數(shù)分布里面的意義基本是一樣的彤断,也是在一個時間段內事件平均發(fā)生的次數(shù)。
泊松分布表示的是事件發(fā)生的次數(shù)易迹,“次數(shù)”這個是離散變量宰衙,所以泊松分布是離散隨機變量的分布。
指數(shù)分布是兩件事情發(fā)生的平均間隔時間睹欲,“時間”是連續(xù)變量供炼,所以指數(shù)分布是一種連續(xù)隨機變量的分布。
可以用等公交車作為例子:
某個公交站臺一個小時內出現(xiàn)了的公交車的數(shù)量 就用泊松分布來表示
某個公交站臺任意兩輛公交車出現(xiàn)的間隔時間 就用指數(shù)分布來表示