最近拜讀西瓜教授的西瓜書医男,讀到神經(jīng)網(wǎng)絡(luò)章節(jié)的時候滑绒,看到了一個神奇的現(xiàn)象。書中骚勘,畫出了一個神經(jīng)網(wǎng)絡(luò)迭代25次铐伴、50次和100次分別得到的分類邊界圖,令人驚訝的是分類邊界在給定范圍內(nèi)都是直線俏讹!一直以來当宴,對神經(jīng)網(wǎng)絡(luò)分類邊界的認(rèn)識是很模糊的,潛意識覺得應(yīng)該是一個很復(fù)雜且直觀無法解釋的東西泽疆。(呵呵户矢,對線性可分?jǐn)?shù)據(jù)似乎也不需要多復(fù)雜的分類面吼)本能反應(yīng)是,我應(yīng)該把這個分類邊界算一個殉疼,看看是個什么函數(shù)梯浪。
- 書本上的數(shù)據(jù)和圖如下

令最上面一層兩個節(jié)點的輸出相等,可以得到如下公式(由于只是判斷相等株依,最后一層省去Sigmoid函數(shù)運算):
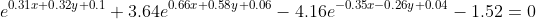
這么復(fù)雜的一個公式驱证,局部作用域竟然是一條直線,有點不可思議恋腕,還是畫出來看看抹锄。

還真的幾乎是一條直線!!不過新的問題來了伙单,這個圖貌似和書本上第25輪迭代時誤分了3個樣本的圖很不一樣获高,這個圖中明顯各個類別的樣本都乖乖的待在自己該待的那一側(cè)。
下面分別看一下第50次迭代和第100次迭代得到的模型參數(shù)畫出來的圖是什么樣吻育。


感覺這三個圖的順序似乎顛倒了念秧,出現(xiàn)這個結(jié)果,首先想到是不是哪里出問題了呢布疼。
- 首先摊趾,驗證公式和模型參數(shù)都是不是正確的。然而游两,以兩種不同的方式將公式的圖像畫出來砾层,是一模一樣的,見附錄的代碼贱案。說明公式和參數(shù)這里基本沒有問題肛炮。
兩種方式分別為: - 手動計算公式如上文
-
以
$$)的形式用code來計算
- 那接下來,自己用相同的樣本來訓(xùn)練網(wǎng)絡(luò)宝踪,畫出其迭代過程中的圖形變化看是否也是這種情況侨糟。既然最近TensorFlow這么火,就趁此機會好好利用一把瘩燥。用TensorFlow搭建的神經(jīng)網(wǎng)絡(luò)迭代過程中的分類邊界的變化情況如下秕重。學(xué)習(xí)率設(shè)置為0.1時,貌似迭代大概1000次才起效果颤芬。經(jīng)本人實踐悲幅,迭代10000次的時候,直線就明顯在兩類數(shù)據(jù)的正中間了站蝠。訓(xùn)練過程也是很坎坷了汰具,試了幾次迭代次數(shù)設(shè)為1000,第1000輪迭代的時候分類面卻差強人意菱魔,不由得有點灰心喪氣留荔,感覺對神經(jīng)網(wǎng)絡(luò)的認(rèn)知有很大的偏差。把迭代次數(shù)調(diào)至10000次后澜倦,終于看到了合理的分類邊界聚蝶。再重復(fù)進(jìn)行實驗,卻發(fā)現(xiàn)1000次也能基本訓(xùn)練出一個合格的分類面藻治,這個過程真是有趣又無解碘勉。



第250輪的圖中沒有曲線可能是因為曲線不在這個范圍中,但是我并沒有設(shè)置畫圖的取值范圍桩卵,難道有一個默認(rèn)取值验靡?這個地方還有待分析倍宾。
由此來看,這個畫圖的過程應(yīng)該是沒有什么問題胜嗓「咧埃或許是理解錯書上的分類機制了?還是周老師給的參數(shù)辞州?怔锌??看來得找個時間跟周老師好好談一談变过。[奸笑]
PS:
MATLAB作圖Code
function ezplotAndscatter()
syms x y
% eq = exp(0.31*x+0.32*y+0.1)+ 3.64*exp(0.66*x + 0.58*y + 0.06) - 4.16*exp(-0.35*x-0.26*y+0.04) - 1.52;
% ezplot(eq);
ezplot(nn);
hold on
a = [0, 1, 1, 0, 2];
b = [0, 0, 1, 2, 2];
c = [1, -1, -1, -1, -1];
scatter(a,b,'filled', 'cdata', c);
end
function eq = nn()
syms x y
X = [x; y];
%%%%%%% Data from ML book
% %%%%%%% Iter 25
% W1 = [-0.66 -0.58; 0.35 0.26];
% b1 = [-0.06; -0.04];
% W2 = [0.63 -0.34; -0.66 0.32];
% b2 = [-0.11; 0.14];
% %%%%%%% Iter 50
% W1 = [-1.56 -1.4; 1.3 1.11];
% b1 = [-0.96; 0.53];
% W2 = [2.0 -1.68; -2.02 1.65];
% b2 = [-0.49; 0.51];
% %%%%%% Iter 100
% W1 = [-1.5 -2.6; 1.36 2.11];
% b1 = [-2.27; 1.72];
% W2 = [3.3 -2.8; -3.33 2.77];
% b2 = [-0.53; 0.56];
%%%%%%% Data from TensorFlow Result
% %%%%%%% Iter 250
% W1=[-1.26210248, -0.25560322; -0.3448638, -1.05593634];
% b1=[-1.71526241; -0.26877293];
% W2=[-0.00534603, 0.66253644; -0.56399935, -1.31708527];
% b2=[-1.31086206; 1.47235668];
% %%%%%% Iter 500
% W1=[-1.29343784, -0.31103003; -0.77500188, -1.32072091];
% b1=[-1.62698305; 0.12957691];
% W2=[0.1474047, 1.09768057; -0.71989417, -1.74458826];
% b2=[-1.42118454; 1.55051541];
%%%%%%% Iter 1000
W1=[-1.40092099, -0.46792907; -1.99782729, -1.86098731];
b1=[-1.34137416; 1.03618503];
W2=[0.49490803, 2.38475251; -1.02381837, -2.8431468];
b2=[-1.66594923; 1.86549616];
Ksi = sigmoid(W1*X + b1);
% O = sigmoid(W2*Ksi + b2);
O = W2*Ksi + b2;
eq = O(1,1) - O(2,1);
end
function A = sigmoid(x)
A = 1./(1+exp(-x));
end
TensorFlow訓(xùn)練神經(jīng)網(wǎng)絡(luò)
import numpy as np
import tensorflow as tf
# Parameters
learning_rate = 0.1
batch_size = 100
display_step = 1
#model_path = "/home/lei/TensorFlow-Examples-master/examples/4_Utils/model.ckpt"
# Network Parameters
n_hidden_1 = 2 # 1st layer number of features
n_input = 2 # MNIST data input (img shape: 28*28)
n_classes = 2 # MNIST total classes (0-9 digits)
# tf Graph input
xs = tf.placeholder("float", [None, n_input])
ys = tf.placeholder("float", [None, n_classes])
# Create model
def multilayer_perceptron(x, weights, biases):
# Hidden layer with RELU activation
layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1'])
layer_1 = tf.sigmoid(layer_1)
# Output layer with linear activation
out_layer = tf.add(tf.matmul(layer_1, weights['out']), biases['out'])
out_layer = tf.sigmoid(out_layer)
return out_layer
# Store layers weight & bias
weights = {
'h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
'out': tf.Variable(tf.random_normal([n_hidden_1, n_classes]))
}
biases = {
'b1': tf.Variable(tf.random_normal([n_hidden_1])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
# Construct model
prediction = multilayer_perceptron(xs, weights, biases)
x_data = np.array([[0,0],[1,0],[1,1],[0,2],[2,2]])
y_data = np.array([[1, 0],[0, 1],[0, 1],[0, 1],[0,1]])
# x_data = np.linspace(-1,1,300)[:, np.newaxis]
# noise = np.random.normal(0, 0.05, x_data.shape)
# y_data = np.square(x_data) - 0.5 + noise
# 4.定義 loss 表達(dá)式
# the error between prediciton and real data
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
reduction_indices=[1]))
# 5.選擇 optimizer 使 loss 達(dá)到最小
# 這一行定義了用什么方式去減少 loss埃元,學(xué)習(xí)率是 0.1
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# important step 對所有變量進(jìn)行初始化
# init = tf.initialize_all_variables()
init = tf.global_variables_initializer()
sess = tf.Session()
# 上面定義的都沒有運算,直到 sess.run 才會開始運算
sess.run(init)
# 迭代 1000 次學(xué)習(xí)媚狰,sess.run optimizer
for i in range(1000):
# training train_step 和 loss 都是由 placeholder 定義的運算亚情,所以這里要用 feed 傳入?yún)?shù)
sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
if i % 250 == 0:
print(i)
#print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))
print(sess.run(weights), sess.run(biases))
print(sess.run(weights), sess.run(biases))