[TOC]

思路框架

在描述統(tǒng)計(jì)中，正態(tài)分布的一組數(shù)據(jù)有兩個(gè)最重要的特征泻轰，一個(gè)是如何集中的（均值$\mu$）寝优，另一個(gè)是如何離散的(方差$\sigma^2$)晃危。據(jù)此可以劃分出大部分?jǐn)?shù)據(jù)存在的范圍（95%的數(shù)據(jù)位于$(\mu-1.96\sigma,\mu+1.96\sigma)$的命中區(qū)間之內(nèi)）。不同數(shù)據(jù)可以放在同一個(gè)參考系（標(biāo)準(zhǔn)分$z=\cfrac {x-\mu} \sigma$）中比較梨水。

推論統(tǒng)計(jì)是通過(guò)部分?jǐn)?shù)據(jù)（樣本）的特征（樣本統(tǒng)計(jì)量拭荤，樣本均值$\bar x$或樣本方差$s^{2$），來(lái)推測(cè)估計(jì)全體數(shù)據(jù)（正態(tài)總體）的特征（總體參數(shù)冰木，總體均值$\mu$或總體方差$\sigma}2$）穷劈。這個(gè)推測(cè)的可信程度（置信區(qū)間）是運(yùn)用假設(shè)檢驗(yàn)的方法來(lái)確認(rèn)的，即能夠讓樣本統(tǒng)計(jì)量的觀測(cè)值進(jìn)入命中區(qū)間的總體參數(shù)才能被接受踊沸。解滿足命中區(qū)間（$上界 \leq 公式 \leq 上界$）的不等式即可歇终。

若估計(jì)$\mu$：

|條件|公式|分布
|--
|已知$\sigma^2$|$\cfrac {\bar x - \mu} {\cfrac \sigma {\sqrt n}}$|$\bar x$呈正態(tài)分布
|未知$\sigma^2$|$\cfrac {(\bar x - \mu) \sqrt {n-1}} s$|$\bar x$呈自由度$(n-1)$的t分布

若估計(jì)$\sigma^2$：

|條件|公式|分布
|--
|已知$\mu$|$\sum _{i=1} ^n (\cfrac {x_i-\mu} \sigma)^2$|$\sigma2$呈自由度$n$的卡方分布
|未知$\mu$|$\cfrac {ns^2} {\sigma^2}$|$s2$呈自由度$(n-1)$的卡方分布

通過(guò)繪制直方圖，可以直觀的反映出數(shù)據(jù)（樣本統(tǒng)計(jì)量的觀測(cè)值）與其出現(xiàn)的相對(duì)頻數(shù)（概率）之間的關(guān)系逼龟，即置信區(qū)間（觀測(cè)值的命中區(qū)間）與概率密度曲線下的面積（相對(duì)頻數(shù)之和）之間的關(guān)系评凝。越趨近于曲線中部的數(shù)據(jù)出現(xiàn)的概率越大，在曲線尾部的數(shù)據(jù)幾乎不可能出現(xiàn)腺律。以此可作為在假設(shè)檢驗(yàn)中接受推論假設(shè)（$|統(tǒng)計(jì)量|>臨界值$奕短，或$p<\alpha$）的依據(jù)。

均值匀钧、方差

統(tǒng)計(jì)量是指用一個(gè)數(shù)來(lái)概括一組數(shù)據(jù)的特征翎碑。樣本的統(tǒng)計(jì)量對(duì)應(yīng)于總體參數(shù)。

例：投一組硬幣之斯。每次投5枚就是5個(gè)樣本日杈，即觀測(cè)這一組樣本的數(shù)量（統(tǒng)計(jì)量）為5枚。一共投了4次，則總的觀測(cè)數(shù)量（總體參數(shù)）為20枚莉擒。

均值$\mu$（算術(shù)平均值）是合計(jì)意義上的平均數(shù)酿炸。
$$\mu=\frac 1 n \sum_{i=1}^n x_i=\sum 組值 \times 相對(duì)頻數(shù)$$

方差$\sigma^2$反映了數(shù)據(jù)的分散（波動(dòng)）程度。
$$\sigma^2 = \frac 1 n \sum_{i=1}^n (x_i - \mu)^2=\sum (組值-\mu)^2 \times 相對(duì)頻數(shù)$$
其中涨冀，$x_i - \mu$稱為偏差填硕，$\sigma$稱為標(biāo)準(zhǔn)差，即方差的開(kāi)平方鹿鳖。

例：制作頻數(shù)分布表扁眯，并計(jì)算$\mu$、$\sigma^2$

|數(shù)據(jù)分組|組值|頻數(shù)|相對(duì)頻數(shù)|累積頻數(shù)|累積相對(duì)頻數(shù)
|--
|1,2,3|2|3|0.3|3|0.3
|4,5,5,5,6|5|5|0.5|8|0.8
|8,8|8|2|0.2|10|1.0

相對(duì)頻數(shù)為各組頻數(shù)占全體的比例栓辜。各組相對(duì)頻數(shù)之和為1恋拍。

$$
\begin{split}
\mu & = \frac{\sum 組值\times頻數(shù)} {數(shù)據(jù)總數(shù)} \
& = \sum 組值 \times \frac{頻數(shù)} {數(shù)據(jù)總數(shù)} \
& = \sum 組值 \times 相對(duì)頻數(shù) \
& = 2\times0.3 + 5\times0.5 + 8\times0.2 \
& = 4.7
\end{split}
$$
$$
\begin{split}
\sigma^2 & = \sum (組值-\mu)^2 \times 相對(duì)頻數(shù) \
& = (2-4.7)^2 \times 0.3 + (5-4.7)^2 \times 0.5 + (8-4.7)^2 \times 0.2 \
& = 4.41
\end{split}
$$

以觀測(cè)的數(shù)據(jù)為橫軸，其相對(duì)頻數(shù)為縱軸藕甩，畫出直方圖施敢，可知：

• 數(shù)據(jù)在$\mu$周邊分布，多次出現(xiàn)的數(shù)據(jù)對(duì)$\mu$影響較大
• 若直方圖左右對(duì)稱狭莱，對(duì)稱軸在$\mu$上

$\mu$是從數(shù)據(jù)的分布中取出的代表數(shù)僵娃，可認(rèn)為數(shù)據(jù)以$\mu$為基點(diǎn)，左右擴(kuò)散腋妙。評(píng)價(jià)這種擴(kuò)散默怨、分散的標(biāo)準(zhǔn)就是$\sigma$。$\sigma$將$\mu$的離散方式進(jìn)行平均化骤素。此時(shí)無(wú)論是正方向匙睹，還是負(fù)方向的離散，都用正數(shù)進(jìn)行評(píng)價(jià)济竹，避免相互抵消的平均痕檬。

例：全班考試成績(jī)$\mu=60$，某人成績(jī)$x=85$送浊。當(dāng)$\sigma=20$時(shí)梦谜，這是一般的水平。當(dāng)$\sigma=10$時(shí)袭景，那就是優(yōu)秀了唁桩。

$\mu$與$\sigma$有如下性質(zhì)：
|統(tǒng)計(jì)量|$\mu$|$\sigma^2$|$\sigma$
|--
|加上常數(shù)$c$|$\mu+k$|$\sigma^2$|$\sigma$
|擴(kuò)大常數(shù)$k$|$\mu \times k$|$\sigma^2 \times k^2$|$\sigma \times k$

全部數(shù)據(jù)經(jīng)過(guò)標(biāo)準(zhǔn)分$z$處理可得，$\mu=0$耸棒，$\sigma=1$荒澡。相當(dāng)于為不同數(shù)據(jù)之間的比較建立了統(tǒng)一的參考系。顯然与殃，$1\sigma$的數(shù)據(jù)比$2\sigma$的數(shù)據(jù)更具代表性单山。

$$z=\cfrac {x - \mu} \sigma$$

例：甲乙球員的命中率$\mu$分別 為70捏肢，40，$\sigma$分別為20饥侵，10。本次訓(xùn)練的命中率$x$分別為75衣屏，55躏升。則$z$分別為$\cfrac {75-70} {20}=0.25<1$，$\cfrac {55-40} {10}=1.5>1$狼忱。故甲球員的命中率更穩(wěn)定膨疏。

其它類型的平均值：
幾何平均值$\bar x = \sqrt [n] {\prod {i=1} ^n x_i}$
均方根值$x{rms} = \sqrt {\cfrac 1 n \sum _{i=1} ^n x_i ^2}$
調(diào)和平均值$H=\cfrac n {\sum _{i=1} ^n \cfrac 1 x_i}$
加權(quán)平均值$\bar x = \cfrac {\sum _{i=1} ^n w_i x_i} {\sum _{i=1} ^n w_i}$

正態(tài)分布

制作直方圖的過(guò)程，其實(shí)就是數(shù)數(shù)钻弄，確定觀測(cè)值與頻數(shù)的關(guān)系佃却。將直方圖中分組幅度無(wú)限縮小，得到$x$的正態(tài)分布圖窘俺。這是由部分事實(shí)推論全體的歸納推論饲帅。

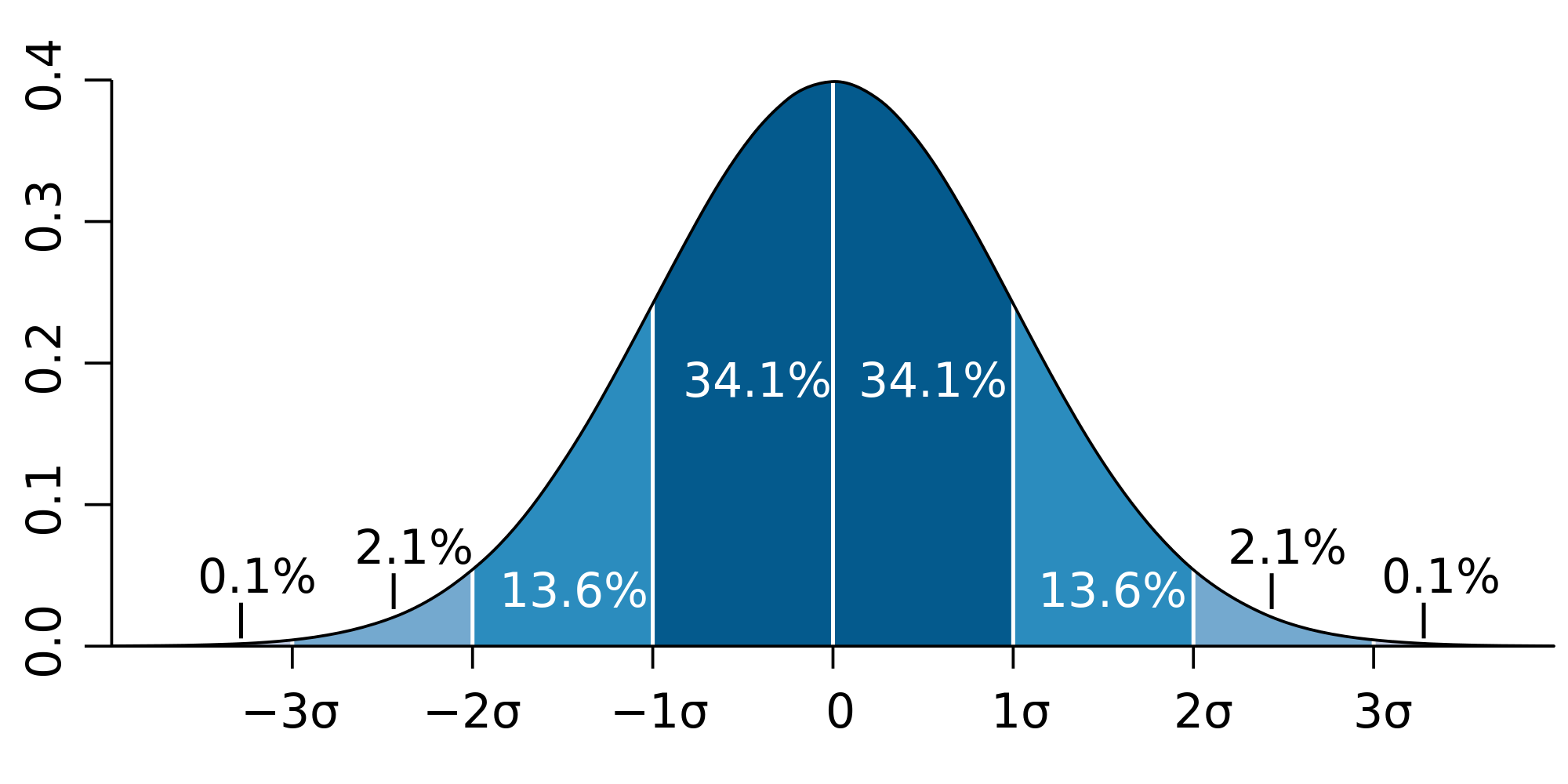
由圖可知，正態(tài)分布確定了觀測(cè)值$x$瘤泪、曲線位置$\mu$灶泵、曲線形狀$\sigma$三者與相對(duì)頻數(shù)$z$之間的關(guān)系：

$$
z = \cfrac {x-\mu} \sigma
$$

當(dāng)$\mu=0$，$\sigma=1$時(shí)对途，稱為標(biāo)準(zhǔn)正態(tài)分布赦邻。性質(zhì)如下：

• 概率密度函數(shù)關(guān)于$\mu$對(duì)稱
• $\mu$、中位數(shù)实檀、眾數(shù)惶洲，三者相等
• 曲線之下的面積（相對(duì)頻數(shù)之和）恒等于1。$(\mu-1\sigma,\mu+1\sigma)$區(qū)間的面積0.6826（70%弱）膳犹，$(\mu-2\sigma,\mu+2\sigma)$區(qū)間的面積0.9544（95%強(qiáng)）恬吕，$(\mu-1.96\sigma,\mu+1.96\sigma)$區(qū)間的面積0.95

推廣到一般正態(tài)分布，

• 當(dāng)$\mu<0$時(shí)镣奋，曲線左移币呵。當(dāng)$\mu>0$時(shí)，曲線右移
• 當(dāng)$\sigma^{2<1$時(shí)侨颈，曲線高且窄余赢。當(dāng)$\sigma}2>1$時(shí)，曲線平且寬
• 通過(guò)$z$回歸到標(biāo)準(zhǔn)正態(tài)分布

例：一次性投$n$枚硬幣哈垢，正面的數(shù)量近似于$\mu=\cfrac n 2$妻柒，$\sigma=\cfrac {\sqrt n} 2$的正態(tài)分布。

利用正態(tài)分布的性質(zhì)耘分，在95%區(qū)間(正態(tài)曲線面積為0.95）上举塔，以$-1.96 \leq \cfrac {x-\mu} \sigma \leq +1.96$為工具绑警，有三種類型的應(yīng)用：

• 已知$\mu$與$\sigma$，預(yù)測(cè)$x$的取值范圍央渣，即命中區(qū)間
• 已知$x$與$\sigma$计盒，檢驗(yàn)$\mu$的合理性，即假設(shè)檢驗(yàn)
• 已知$x$與$\sigma$芽丹，估計(jì)$\mu$的取值范圍北启，即置信區(qū)間

命中區(qū)間

預(yù)測(cè)命中區(qū)間，是在總體參數(shù)$\mu$與$\sigma$已知的情況下拔第，針對(duì)未發(fā)生事件$x$的預(yù)測(cè)咕村。

例：一次投$n=36$枚硬幣，預(yù)測(cè)正面的數(shù)量$x$的范圍蚊俺。
由正態(tài)分布可知懈涛，$\mu=\cfrac n 2 =\cfrac {36} 2=18$，$\sigma= \cfrac {\sqrt n} 2 =\cfrac {\sqrt {36}} 2=3$泳猬。解不等式
$$
\begin{gather}
-1.96 \leq \cfrac {x-\mu} \sigma \leq +1.96 \
-1.96 \leq \cfrac {x-18} 3 \leq +1.96 \
12.12 \leq x \leq 23.88
\end{gather}
$$
結(jié)論為批钠，一次投36枚硬幣，有95%的可能性得封，正面數(shù)量在12到24枚价匠。

假設(shè)檢驗(yàn)

假設(shè)檢驗(yàn)中，假設(shè)是指“關(guān)于總體的一個(gè)普遍性論斷”呛每，檢驗(yàn)是指“看從樣本得出的結(jié)論能否推論到總體”踩窖。假設(shè)檢驗(yàn)的邏輯是，命題只能被證否而不能被證明晨横。個(gè)案（樣本）不足以證明命題（總體）洋腮，但可以否定命題（總體）。

1. 首先設(shè)置一個(gè)關(guān)于總體的假設(shè)手形，稱為虛無(wú)假設(shè)$H_0$啥供。然后設(shè)置$H_0$的否命題，稱為備選假設(shè)$H_1$库糠。如果證否了$H_0$伙狐，相當(dāng)于證明了$H_1$。所以假設(shè)檢驗(yàn)就是要試圖證否$H_0$瞬欧，或者說(shuō)拒絕$H_0$（無(wú)法拒絕就只能接受）
2. 由于抽樣的原因贷屎，樣本并不可能絕對(duì)地證否$H_0$。在個(gè)案中艘虎，小概率事件可以等同于不可能發(fā)生的事件唉侄。在此意義上，需要事先約定在一個(gè)錯(cuò)誤概率（即顯著水平$\alpha$）上去拒絕$H_0$（有$\alpha$的可能性推論錯(cuò)誤）

例：若有$10$枚硬幣正面野建，則一次投出的硬幣數(shù)量$n=36$是否合理属划？

第一步：構(gòu)建假設(shè)
$H_0$：$n=36$恬叹，硬幣總量為36枚
$H_1$：$n \neq 36$，硬幣總量不是36枚

第二步：設(shè)置檢驗(yàn)顯著水平
$\alpha = 0.05$（即雙側(cè)位于$(\mu -1.96\sigma , \mu +1.96\sigma)$之外的曲線面積同眯，$1-\alpha$為95%置信水平）绽昼。從正態(tài)圖上看，$\cfrac \alpha 2$對(duì)應(yīng)的坐標(biāo)稱為臨界值须蜗。觀測(cè)值$x$對(duì)應(yīng)的面積稱為統(tǒng)計(jì)量$p$值绪励。

第三步：計(jì)算統(tǒng)計(jì)量進(jìn)行檢驗(yàn)判斷

由正態(tài)分布可知，$\mu=\cfrac n 2 =\cfrac {36} 2=18$唠粥，$\sigma=\cfrac {\sqrt n} 2 =\cfrac {\sqrt {36}} 2=3$。因$觀測(cè)值x=10 < 18=\mu$停做，故樣本位于$\mu$的左側(cè)晤愧。

一種方法是比較觀測(cè)值與臨界值。
由$左側(cè)臨界值=\mu - 1.96\sigma = 18 - 1.96 \times 3=12.12$可知蛉腌，$觀測(cè)值x=10 < 12.12=臨界值$官份。

另一種方法是比較$p$與$\alpha$。
由$\cfrac {x-\mu} \sigma = \cfrac {10- 18} 3 = -2.67$烙丛，查正態(tài)分布表或公式函數(shù)計(jì)算可知對(duì)應(yīng)面積為$0.9962$舅巷。在左側(cè)，$p =1 - 0.9962 = 0.0038 < 0.025 = \cfrac {0.05} 2 = \cfrac \alpha 2$河咽。

第四步：得出結(jié)論
如果要拒絕$H_0$钠右，即在$H_0$出現(xiàn)了小概率事件（不太可能發(fā)生的事件），滿足以下條件之一即可：

• 比較觀測(cè)值與臨界值忘蟹，若樣本位臨界值范圍之外
• 比較$p$與$\alpha$飒房，若$p<\alpha$（雙側(cè)），或$p < \cfrac \alpha 2$（單側(cè)）

結(jié)論為媚值，一次投36枚硬幣出現(xiàn)10枚正面狠毯，屬于小概率事件（0.38%的可能性，不太可能發(fā)生）褥芒，故硬幣數(shù)量不合理嚼松。這個(gè)結(jié)論有5%的可能性出錯(cuò)。

置信區(qū)間

區(qū)間估計(jì)是指锰扶，在樣本已知的情況下献酗，推測(cè)未知真實(shí)值的總體參數(shù)的取值范圍。以一定固定結(jié)構(gòu)概率性出現(xiàn)的是樣本觀測(cè)值坷牛，而總體參數(shù)真實(shí)值是確切的凌摄，只是不知道是多少，但會(huì)有一定的概率落在樣本的取值范圍內(nèi)漓帅。置信區(qū)間表達(dá)了對(duì)出現(xiàn)的觀測(cè)值的可信程度（即總體參數(shù)會(huì)落在樣本命中區(qū)間的概率的可信程度）锨亏。從針對(duì)總體參數(shù)的假設(shè)檢驗(yàn)可知痴怨，在排除了$\alpha$的錯(cuò)誤概率后，剩下的$1-\alpha$就是觀測(cè)值出現(xiàn)概率的可信程度器予。$1-\alpha$對(duì)應(yīng)的區(qū)間就是置信區(qū)間浪藻。

從正態(tài)分布圖上看，全部觀測(cè)值$x$中乾翔，有95%出現(xiàn)在$(\mu-1.96\sigma,\mu+1.96\sigma)$之內(nèi)爱葵。總體參數(shù)$\mu$也落在這個(gè)區(qū)間內(nèi)的可信程度有95%反浓。稱之為萌丈，由95%的樣本觀測(cè)值$x$構(gòu)造的總體參數(shù)$\mu$的置信區(qū)間。

例：若有$10$枚硬幣正面雷则，則一次投出的硬幣數(shù)量$n$有多少辆雾？
由正態(tài)分布可知，$\mu=\cfrac n 2$月劈，$\sigma=\cfrac {\sqrt n} 2$度迂，觀測(cè)值$x=10$。$\mu$的95%置信區(qū)間滿足：
$$
\begin{gather}
-1.96 \leq \cfrac {x-\mu} \sigma \leq +1.96 \
-1.96 \leq \cfrac {10 - \cfrac n 2} {\cfrac {\sqrt n} 2} \leq +1.96 \
12.95 \leq n \leq 30.89
\end{gather}
$$
結(jié)論為猜揪，有10枚硬幣正面惭墓，則有95%的把握說(shuō)，一次投出的硬幣數(shù)量在13到30枚之間而姐。

大數(shù)法則腊凶、中心極限定理

推論統(tǒng)計(jì)的目標(biāo)是，從總體數(shù)據(jù)抽樣出來(lái)的樣本數(shù)據(jù)中拴念，對(duì)總體的數(shù)據(jù)特征進(jìn)行推測(cè)吭狡。如果不假設(shè)總體的分布，可以采用非參數(shù)統(tǒng)計(jì)丈莺。如果假設(shè)總體為正態(tài)分布划煮，則可以采用大樣本估計(jì)。

從制作直方圖的過(guò)程中缔俄，抽取一組樣本（分組）弛秋，取其組值（樣本均值$\bar x$），可以觀察到：

• 相對(duì)頻數(shù)反映了總體數(shù)據(jù)的構(gòu)成情況俐载。換言之蟹略，樣本的觀測(cè)值$x$的分布是受總體的數(shù)據(jù)特征制約的
• 從$\bar x$的漸近趨勢(shì)上看，當(dāng)抽樣數(shù)量越多遏佣，$\bar x$接近總體均值$\mu$的可能性越高挖炬。這就是大數(shù)法則
• 從$\bar x$的數(shù)據(jù)分布上看，當(dāng)抽樣數(shù)量越多状婶，$\bar x$分布越近似于正態(tài)分布意敛。這就是中心極限定理

由此推論：正態(tài)總體取$n$個(gè)樣本均值$\bar x$的分布仍為正態(tài)分布馅巷。

例：投一組硬幣正面的數(shù)量，身高草姻，股票價(jià)格等現(xiàn)象钓猬，均表現(xiàn)為正態(tài)分布。

從正態(tài)圖形上撩独，比較樣本觀測(cè)值$x$敞曹，與樣本均值$\bar x$的分布：

|分布（直方圖橫軸上的觀測(cè)值）|均值|標(biāo)準(zhǔn)差|形狀
|--
|$x$|$\mu$|$\sigma$|平且寬
|$\bar x$|$\mu$|$\cfrac \sigma {\sqrt n}$|高且窄

由正態(tài)分布性質(zhì)可知，對(duì)于均值為μ综膀、標(biāo)準(zhǔn)差為σ的一個(gè)正態(tài)總體的n個(gè)樣本均值$\bar x$來(lái)說(shuō)澳迫，其95%預(yù)測(cè)命中區(qū)間為：
$$-1.96 \leq \cfrac {\bar x - \mu} {\cfrac \sigma {\sqrt n}} \leq +1.96$$

例：若正態(tài)總體的$\mu=200$，$\sigma=10$時(shí)剧劝，樣本數(shù)量$n$分別為1橄登，4，16担平，預(yù)測(cè)95%命中區(qū)間，分別為(180.4 , 219.6)锭部，(190.2 , 209.8)暂论，(195.1 , 204.9)“韬蹋可見(jiàn)觀測(cè)數(shù)據(jù)越多取胎，預(yù)測(cè)區(qū)間越狹窄，預(yù)測(cè)精度越高湃窍。

正態(tài)總體闻蛀，已知總體方差，估計(jì)總體均值

由樣本均值$\bar x$的正態(tài)分布性質(zhì)您市，可推測(cè)總體參數(shù)$\mu$的置信區(qū)間觉痛。實(shí)施假設(shè)檢驗(yàn)，能夠讓樣本均值$\bar x$進(jìn)入預(yù)測(cè)命中區(qū)間的總體均值$\mu$茵休，才能被授受薪棒。這個(gè)區(qū)間就是總體均值$\mu$的置信區(qū)間。

例：一批產(chǎn)品的重量允許有平均10克的浮動(dòng)榕莺，從中抽取25個(gè)樣品俐芯，其樣品的平均重量80克。則這些產(chǎn)品的平均重量$\mu$有多少克钉鸯？

由樣本均值正態(tài)分布可知吧史，$n=25$，$\sigma=10$唠雕，$\bar x=80$贸营。$\mu$的95%置信區(qū)間滿足：

$$
\begin{gather}
-1.96 \leq \cfrac {\bar x - \mu} {\cfrac \sigma {\sqrt n}} \leq +1.96 \
-1.96 \leq \cfrac {80 - \mu} {\cfrac {10} {\sqrt {25}}} \leq +1.96 \
76.08 \leq \mu \leq 83.92
\end{gather}
$$
結(jié)論為吨述，這批產(chǎn)品平均重量在76.08至83.92克之間的可信度為95%。

正態(tài)總體莽使，已知總體均值锐极，估計(jì)總體方差——卡方分布

在一般正態(tài)總體中抽取$n$個(gè)樣本，將方差公式中的$\sum _{i=1} ^n (x_i - \mu)^2$這一部分芳肌，使用$\cfrac {x_i - \mu} \sigma$標(biāo)準(zhǔn)化灵再。計(jì)算統(tǒng)計(jì)量$\chi^2=\sum _{i=1} ^n (\cfrac {x_i - \mu} \sigma)^2$的值，作為直方圖的橫軸觀測(cè)數(shù)據(jù)亿笤，得到正態(tài)總體的總體方差的自由度$n$的卡方分布翎迁。

卡方分布的圖形呈過(guò)山車形：

• 由于平方和形式，曲線位于第一象限净薛，故不是正態(tài)分布
• 卡方分布由正態(tài)分布構(gòu)造汪榔，不同的自由度，就是不同的曲線
• 0附近的相對(duì)頻數(shù)較大肃拜，曲線從左到右下落
• 隨著自由度增加痴腌，遠(yuǎn)離0的相對(duì)頻數(shù)增高，曲線的高度向右變低燃领，近似于正態(tài)分布

例：正態(tài)總體的$\mu=80$士聪，抽取76、85猛蔽、83三個(gè)樣本剥悟。求$\sigma^2$的置信區(qū)間。
查表可知曼库，自由度3的卡方分布区岗，左側(cè)$\cfrac \alpha 2 = 0.975$以上面積為0.2157，右側(cè)$\cfrac \alpha 2 = 0.025$以上面積為9.3484毁枯。根據(jù)假設(shè)檢驗(yàn)慈缔，能夠使卡方值在95%命中區(qū)間的$\sigma^2$才能被接受：
$$
\begin{gather}
0.2157 \leq \sum _{i=1} ^n (\cfrac {x_i-\mu} \sigma)^2 \leq 9.3484 \
0.2157 \leq \cfrac {(76-80)^2 + (85-80)^2 + (83-80)^2} {\sigma^2} \leq 9.3484 \
5.34 \leq \sigma^2 \leq 231.80
\end{gather}
$$

正態(tài)總體，未知總體均值种玛，估計(jì)總體方差

在一般正態(tài)總體中抽取$n$個(gè)樣本胀糜，在方差公式中使用樣本均值$\bar x$，然后加入總體方差$\sigma^2$參與變換蒂誉，可得樣本方差：
$$s^2 = \frac 1 n \sum_{i=1}^n (x_i - \bar x)^2=\cfrac {\sigma^2} n \sum _{i=1} ^n (\cfrac {x_i-\bar x} \sigma)^2$$

可證明教藻，統(tǒng)計(jì)量$\chi^2=\sum _{i=1} ^n (\cfrac {x_i-\bar x} \sigma)^2= \cfrac {ns^2} {\sigma^2}$為正態(tài)總體的樣本方差的自由度$(n-1)$的卡方分布。

例：取一批零件的5個(gè)樣品右锨，重量分別為76括堤，85，82，80悄窃，77克讥电，則這批零件重量的平均浮動(dòng)范圍是多少？
樣品$\bar x=\cfrac {\sum _{i=1} ^n x_i} n=\cfrac {76+85+82+80+77} 5=80$克轧抗。
樣品$s^2=\cfrac 1 n \sum _{i=1} ^n (x_i - \bar x)^2 = \cfrac {(76-80)^2 + (85-80)^2+(82-80)2 + (80-80)^2 + (77-80)^2} 5 = 10.8$克恩敌。
查卡方分布表可知，自由度$(n-1)=5-1=4$的卡方分布的95%命中區(qū)間滿足：
$$
\begin{gather}
0.4844 \leq \cfrac {ns^2} {\sigma^2} \leq 11.1433 \
0.4844 \leq \cfrac {5 \times 10.8} {\sigma^2} \leq 11.1433 \
2.2 \leq \sigma \leq 10.6
\end{gather}
$$
結(jié)論為横媚，這批零件重量平均浮動(dòng)在2.2到10.6克之間纠炮，可信度為95%。

正態(tài)總體灯蝴，未知總體方差恢口，估計(jì)總體均值——t分布

在正態(tài)總體抽取的$n$個(gè)樣本中，樣本均值$\bar x$服從正態(tài)分布穷躁，樣本方差$s^2$服從卡方分布耕肩，可以推導(dǎo)出統(tǒng)計(jì)量：
$$
t=\cfrac {標(biāo)準(zhǔn)正態(tài)分布 \times \sqrt {自由度 - 1}} {\sqrt {卡方分布}} = \cfrac {\cfrac {\bar x - \mu} {\cfrac \sigma {\sqrt n}} \cdot \sqrt {n-1}} {\sqrt {\cfrac {ns^2} {\sigma^2}}} = \cfrac {(\bar x - \mu) \sqrt {n-1}} s
$$
稱為正態(tài)總體的樣本均值$\bar x$的自由度$(n-1)$的t分布。

t分布是以0為中心问潭，左右對(duì)稱的一簇曲線猿诸。與正態(tài)曲線相比更緩和（即山頂略低，山腳略高）狡忙，其形態(tài)變化與自由度$(n-1)$有關(guān)梳虽。自由度越小，曲線越低平去枷；自由度越大怖辆，曲線越接近標(biāo)準(zhǔn)正態(tài)分布曲線是复。這說(shuō)明删顶，當(dāng)$n$并不是足夠大（小樣本）的時(shí)候，t分布和標(biāo)準(zhǔn)正態(tài)分布的偏差不能被忽略淑廊。

例：取一批零件的6個(gè)樣品逗余，重量分別為76，85季惩，82录粱，83，76画拾，78克啥繁，則這批零件平均重量是多少？
樣品$\bar x=\cfrac {\sum _{i=1} ^n x_i} n=\cfrac {76+85+82+83+76+78} 6=80$克青抛。
樣品$s=\sqrt {\cfrac 1 n \sum _{i=1} ^n (x_i - \bar x)^2} = \sqrt {\cfrac {(76-80)^2 + (85-80)^2+(82-80)2 + (83-80)^2 + (76-80)^2 + (78-80)^2} 6} = 3.51$克旗闽。
查t分布表可知，自由度$(n-1)=6-1=5$的t分布的95%命中區(qū)間滿足：
$$
\begin{gather}
-2.571 \leq \cfrac {(\bar x - \mu) \sqrt {n-1}} s \leq +2.571 \ -2.571 \leq \cfrac {(80 - \mu) \sqrt {6-1}} {3.51} \leq +2.571 \
75.964 \leq \mu \leq 80.036
\end{gather}
$$
結(jié)論為，這批零件平均重量在75.964到80.036克之間适室，可信度為95%嫡意。

本書信息

書名：你一定愛(ài)讀的極簡(jiǎn)統(tǒng)計(jì)學(xué)：再精簡(jiǎn)下去，就不是統(tǒng)計(jì)學(xué)了
著者：小島寬之
譯者：孔霈
ISBN：978-7-5168-0451-3