做完這題覺得必須得來個解題報告了,這題的動態(tài)規(guī)劃有點(diǎn)酸爽啊~
問題如下:
編輯距離,又稱Levenshtein距離,是指兩個字串之間图云,由一個轉(zhuǎn)成另一個所需的最少編輯操作次數(shù)。許可的編輯操作包括將一個字符替換成另一個字符,插入一個字符震桶,刪除一個字符。
以上的問題可以用眾所周知的動態(tài)規(guī)劃解決征绎,現(xiàn)在的問題是蹲姐,如果新加入一種編輯操作:交換相鄰的兩個字符;求兩個字符串之間的編輯距離人柿。
輸入為2個字符串(長度小于1000)柴墩,輸出為兩個串的編輯距離。
L氏距離(Levenshtein Distance)
基礎(chǔ)的編輯距離只有3種原子操作:插入1個字符顷扩,刪除1個字符拐邪,更改1個字符.且3種操作的代價均為1.
設(shè)串A為a1 a2 ... am, 串B為b1 b2 ... bn
將串A經(jīng)過n個操作x1 - x2 - ... - xn,使之變成串B隘截,且該操作序列為最優(yōu)操作(代價之和最性住)的一種,則2個串的L氏距離即為該序列代價之和婶芭。通常3個操作的代價都為1,也有可能按某種方案加權(quán)(即3種操作的代價不一致东臀,導(dǎo)致更復(fù)雜的情況,這里只討論都是1的).

這種編輯距離可以很直觀地用DP得到:(同時網(wǎng)絡(luò)上的中文資料大部分都為這種距離)
用C[i,j]表示a1 a2 ... ai到b1 b2 ... bj的距離犀农,則有以下狀態(tài)轉(zhuǎn)移方程:


上面的轉(zhuǎn)移方程是很直觀的惰赋,有人會問這樣每次只考慮對于兩個串的最后一個元素的操作是否會錯過最優(yōu)解,這個可以通過歸納法證明此種求解方法得到的就是最優(yōu)解呵哨。
每個C[i,j]都由下標(biāo)嚴(yán)格小于i和j的元素C[i-1,j-1]/C[i-1,j]/C[i,j-1]決定赁濒。
算法流程即為從左到右,從上到下遍歷矩陣C孟害,最后的整個串的L氏距離值為C[m,n]拒炎。
L氏距離有一些性質(zhì),這里不具體展開了...(-. -!)
D氏距離
<b>1.引子</b>
上面講了那么多挨务,然而并沒有什么卵用击你。
題目中增加了transposition操作玉组,可以交換2個相鄰元素,并且這個操作的代價也是1.那么問題來了丁侄,原先的狀態(tài)轉(zhuǎn)移方程需要如果改變呢惯雳?
最開始我的思路是這樣的,直覺+觀察發(fā)現(xiàn)對于原先方程中的第三個式子鸿摇,在某些條件下石景,若用交換代替原來的操作,可以使總代價減少1:
當(dāng)ai != bj 且 ai-1 != bj-1時:可能通過subs(修改最后一個元素)户辱,從而C[i,j]可能是C[i-1,j-1]+1(也可能是另外2個操作)
若同時ai-1 = bj且ai = bj-1鸵钝,則只需交換最后2個元素即可,則該操作代價應(yīng)比subs少1,從而可排除此輪subs的操作在最優(yōu)操作序列中的可能性庐镐。
<b>2. 2種鏡像操作</b>
這里觀察發(fā)現(xiàn)的交換實(shí)際上只是相鄰2個字符交換的情況恩商,推廣到一般情況,很可能會有如下的操作:
- 交換2個相鄰字符必逆,并在其之間插入字符怠堪。
- 刪除某2個不相鄰字符之間的所有字符,并使之交換名眉。
這2種操作很有可能比原來的代價要低粟矿。
<b>3. 嚴(yán)格編輯距離與D氏距離</b>
另外這里還需要引入另一個概念,所謂嚴(yán)格編輯距離损拢,這個的意思是每次操作只能改變串A的一個位置(最后一個位置)陌粹,嚴(yán)格定義見wiki:optimal string alignment[citation needed] (sometimes called the restricted edit distance[citation needed]
), 我個人理解就是不能往中間插入,每次只能更改串的最后一個字符(或者加入新字符或者刪改原串中的最后一個字符)福压。
這里給了一個例子掏秩,AC 和 CBA 的距離,若是嚴(yán)格編輯距離為4荆姆,則操作為:AC - CA - CB - CBA(或其他)蒙幻;若是D氏距離則為3,操作為AC - CA - CBA,對于刪除同理胆筒。
本題中的“距離”應(yīng)該指的是后者邮破。
<b>4. 最優(yōu)子結(jié)構(gòu)性質(zhì)</b>
L氏距離的DP求解有個性質(zhì),就是某個步驟中的操作一旦被認(rèn)為是最優(yōu)的仆救,則后續(xù)的操作不會再對前面的串再做更改(再更改會使總代價變高)抒和。即存在最優(yōu)子結(jié)構(gòu)。
那D氏距離是否存在最優(yōu)子結(jié)構(gòu)呢彤蔽?
實(shí)際上有個結(jié)論构诚,當(dāng)trans的代價大于等于插入和刪除代價和一半時,trans交換過的元素不會再被更改(Wiki - there always exists an optimal sequence of edit operations, where once-transposed letters are never modified afterwards. (This holds as long as the cost of a transposition,
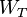

) )
<b>5. 狀態(tài)轉(zhuǎn)移方程</b>
結(jié)合上面幾點(diǎn)铆惑,開了開腦洞范嘱,我想出了這樣的方程


其中,k1和k2一開始我的想法是只要能滿足的交換條件的都去遍歷一遍员魏,實(shí)際上只需要計(jì)算距離當(dāng)前i丑蛤,j最近的一次"交叉相等"即可.(即滿足交叉相等的2個下標(biāo)盡可能大)
由于交換需要的條件是相鄰,因此撕阎,該操作需要先刪除串A中本來存在k1 .. i之間的所有元素受裹,并且在交換k1 .. i之后插入所有B中相應(yīng)的元素,因此就有后面那堆i虏束,k1棉饶,j,k2的運(yùn)算镇匀。
為什么是最“近”呢照藻?
假設(shè)存在一個比較“遠(yuǎn)”的
k3/k4滿足交換條件,即A[k3] = B[j] & A[i] = B[k4],且有 k3 + k4 < k1 + k2汗侵。這里就考慮A中的元素
A[k3+1 .. k1-1]和 B中的 B[k4+1 .. k2-1]幸缕,相信你已經(jīng)想到了,比較近的方案中晰韵,這些元素都尋求最優(yōu)的操作发乔。而較遠(yuǎn)的方案中,采取的是刪除A中元素雪猪,插入B中元素栏尚,則必定大于或等于最優(yōu)操作。因此只需要選擇最“近”的方案即可只恨。
<b>6. 相信到這里就已經(jīng)可以寫出O(N*M)的算法了</b>
其中译仗,Wiki的算法最為簡潔(是Wiki頁面上的算法2)。
D-L距離