今天我們來講解一下上一篇的課后習(xí)題。
1. 題目
編程實(shí)現(xiàn)把1~9九個(gè)數(shù)字填入九宮格中糠馆,滿足每行、每列和對(duì)角線上的三個(gè)數(shù)字和為15怎憋。如圖所示又碌。
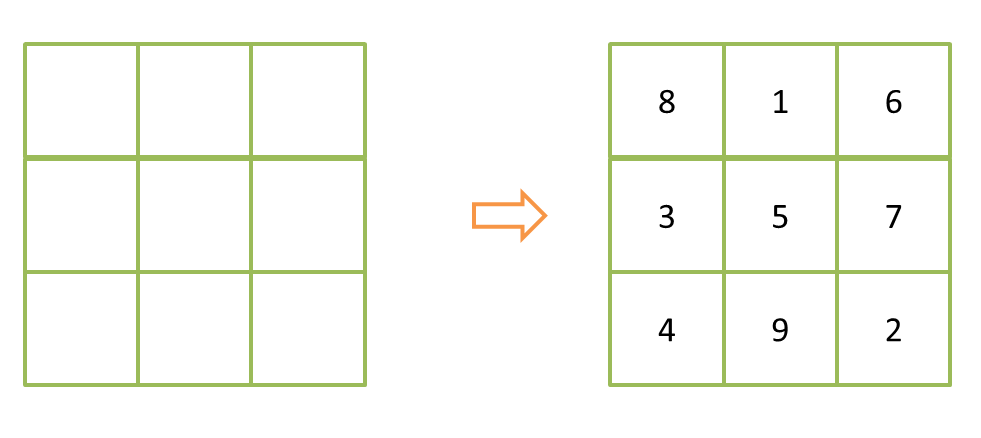
注意:由于結(jié)果不唯一,只要打印出一種滿足條件的結(jié)果即可盛霎。
2. 分析
這道題目很多同學(xué)拿到后覺得無從著手赠橙,完全和學(xué)過的知識(shí)沒有一點(diǎn)聯(lián)系。其實(shí)愤炸,這道題用到的就是學(xué)過的知識(shí)期揪。
2.1 建模
首先,這道題是一個(gè)3 * 3的二維數(shù)組规个,要把9個(gè)數(shù)填進(jìn)去凤薛。在眾多的可能性中找到一個(gè)滿足條件的即可。
接下來诞仓,我們想想之前講到的二維數(shù)組和一維數(shù)組的關(guān)系缤苫,是不是可以把這道題轉(zhuǎn)化成一個(gè)9個(gè)元素的一維數(shù)組,把9個(gè)數(shù)字排列組合放進(jìn)這個(gè)數(shù)組中墅拭。這就和之前拋硬幣的那道題有幾分相像了活玲。

如圖所示,可能出現(xiàn)的情況應(yīng)該共有9!種。我們要做的就是編程窮舉出所有的可能性舒憾,在這個(gè)過程中判斷每種可能性是否滿足題目要求镀钓。
注意:這個(gè)解法并不是最優(yōu)解,但卻是最適合初學(xué)者學(xué)習(xí)的镀迂。我在如何評(píng)價(jià)一段代碼中已經(jīng)闡明了我的觀點(diǎn)丁溅。
2.2 功能分解
有了一個(gè)基本的模型,我們可以把問題轉(zhuǎn)化為幾個(gè)子功能:
- 計(jì)算排列組合
列舉出所有的可能探遵,拿到9!個(gè)二維數(shù)組窟赏。
- 判斷
判斷得到的每個(gè)結(jié)果是否符合要求。
3. 判斷功能
判斷的條件比較簡(jiǎn)單箱季,就是要每行數(shù)字涯穷、每列數(shù)字和兩個(gè)對(duì)角線的數(shù)字之和均為15。大部分人很容易想到這種寫法:
#define MAX_SIZE 3
int g_arr[MAX_SIZE][MAX_SIZE];
int Calculate()
{
int i, j, sum;
// 計(jì)算3行
for (i = 0; i < MAX_SIZE; i++)
{
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[i][j];
}
if (sum != 15)
{
return 0;
}
}
// 計(jì)算3列
for (i = 0; i < MAX_SIZE; i++)
{
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[j][i];
}
if (sum != 15)
{
return 0;
}
}
// 計(jì)算對(duì)角線
sum = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sum += g_arr[i][i];
}
if (sum != 15)
{
return 0;
}
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[i][MAX_SIZE- 1 - j];
}
if (sum != 15)
{
return 0;
}
return 1;
}
Calculate()函數(shù)的功能是判斷二維數(shù)組g_arr是否滿足要求藏雏,如果滿足返回1求豫,如果不滿足返回0。
這個(gè)函數(shù)功能上沒有問題诉稍,但使用了太多次循環(huán),執(zhí)行效率太低最疆。不過細(xì)心的同學(xué)肯定已經(jīng)發(fā)現(xiàn)有些統(tǒng)計(jì)其實(shí)可以合并在一起做杯巨。我對(duì)這段代碼做了優(yōu)化,修改如下:
int Calculate()
{
int i, j;
int sumLine, sumCol, sumDL1, sumDL2;
sumDL1 = 0;
sumDL2 = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sumLine = 0;
sumCol = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sumLine += g_arr[i][j];
sumCol += g_arr[j][i];
}
if (sumLine != 15 || sumCol != 15)
{
return 0;
}
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE- 1 - i];
}
if (sumDL1 != 15 || sumDL2 != 15)
{
return 0;
}
return 1;
}
這段代碼只用了一組嵌套的for循環(huán)努酸,通過四個(gè)變量統(tǒng)計(jì)出了所有數(shù)據(jù)服爷。變量sumLine和sumCol分別用來計(jì)算每一行和每一列的數(shù)字之和。這里只是在循環(huán)中修改了一下i和j的下標(biāo)順序就完成了兩個(gè)維度的統(tǒng)計(jì)获诈。變量sumDL1和sumDL2分別計(jì)算了兩條對(duì)角線上數(shù)字之和仍源。
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE- 1 - i];
這兩行代碼用了在天花板編程手把手計(jì)劃-第1期-第2天中介紹的方法,忘記的同學(xué)可以回去復(fù)習(xí)舔涎。
4. 打印
這里依然需要一個(gè)二維數(shù)組打印的函數(shù)笼踩,這和前面幾個(gè)題目相似,不用多說了亡嫌。
void PrintMap()
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d ", g_arr[i][j]);
}
printf("\n");
}
printf("\n");
}
5. 計(jì)算排列組合
這里依然需要用到一個(gè)遞歸的方法嚎于。每一次遞歸都給一個(gè)對(duì)應(yīng)的位置填寫一個(gè)數(shù)字。這里和拋硬幣問題有一個(gè)唯一的不同挟冠,就是每個(gè)數(shù)字只能填一次于购。
5.1 排除法
Aha_斌同學(xué)是第一個(gè)完成這道題目的,他用的辦法是這樣知染。
首先肋僧,用拋硬幣的方法找出允許重復(fù)情況下的可能矩陣。之后逐一判斷,如果發(fā)現(xiàn)有重復(fù)數(shù)字就舍棄那種情況嫌吠。
這個(gè)解法很聰明止潘,一下就解決了問題,而且不需要太復(fù)雜的算法居兆。代碼大家可以去參考他發(fā)的作業(yè)帖覆山。
5.2 用數(shù)字作遞歸條件
我要介紹的算法是另外一個(gè)思路,不是按照每個(gè)空格去遞歸泥栖,而是按照數(shù)字去遞歸簇宽。通過遞歸的方式執(zhí)行九次動(dòng)作,每次負(fù)責(zé)把一個(gè)數(shù)填在一個(gè)空格中吧享。這樣永遠(yuǎn)不會(huì)出現(xiàn)重復(fù)數(shù)字的問題魏割。
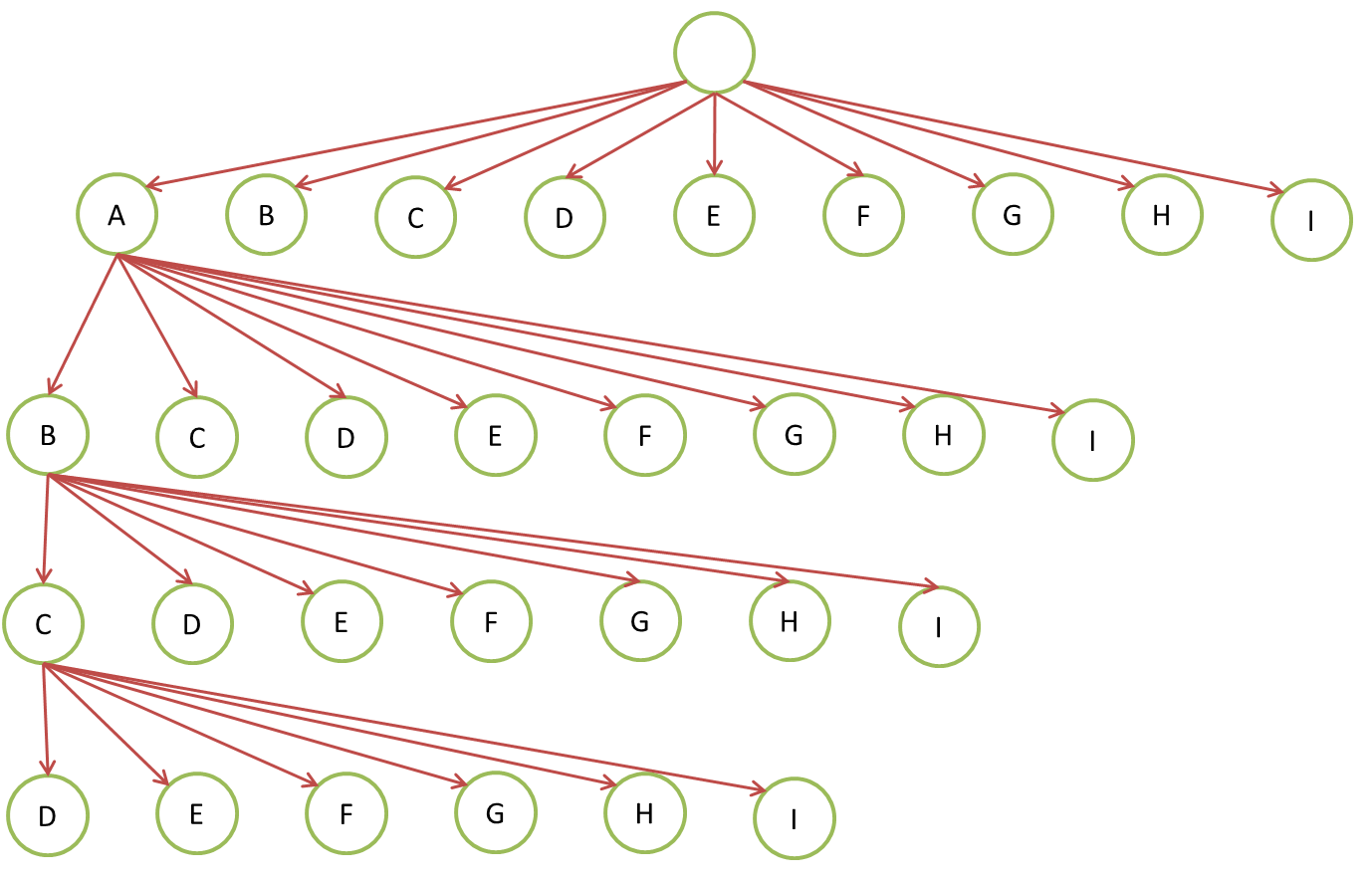
圖中用A~I表示9個(gè)空格,整個(gè)遞歸的過程是一棵不規(guī)則的N叉樹钢颂。根結(jié)點(diǎn)有9個(gè)子節(jié)點(diǎn)钞它,第一層的每個(gè)節(jié)點(diǎn)有8個(gè)子節(jié)點(diǎn),第二層的每個(gè)節(jié)點(diǎn)有7個(gè)子節(jié)點(diǎn)殊鞭,以此類推遭垛。圖中只畫出了一個(gè)分支的前三次迭代。
現(xiàn)在剩下最后一個(gè)問題操灿,每次遞歸時(shí)如何為不同的層執(zhí)行不同次數(shù)的遞歸呢锯仪?
方法一:狀態(tài)恢復(fù)法
另外創(chuàng)建一個(gè)二維數(shù)組紀(jì)錄下當(dāng)前被使用的格子和未使用的格子。每層遞歸函數(shù)返回時(shí)把填寫過的格子更新成未使用的格子趾盐。
這個(gè)方法很容易想庶喜,但要多維護(hù)一個(gè)二維數(shù)組,而且有太多批量賦值的工作救鲤,不適合初學(xué)者久窟。
方法二:利用數(shù)字特性
我使用了一種更巧妙的方法,我先把九個(gè)格子都初始化為0本缠,再讓遞歸按照從大到小的順序填寫數(shù)字斥扛,當(dāng)空格中存在比當(dāng)前數(shù)字小的數(shù)字時(shí),說明這個(gè)格子沒有在這個(gè)分支中被使用過搓茬。
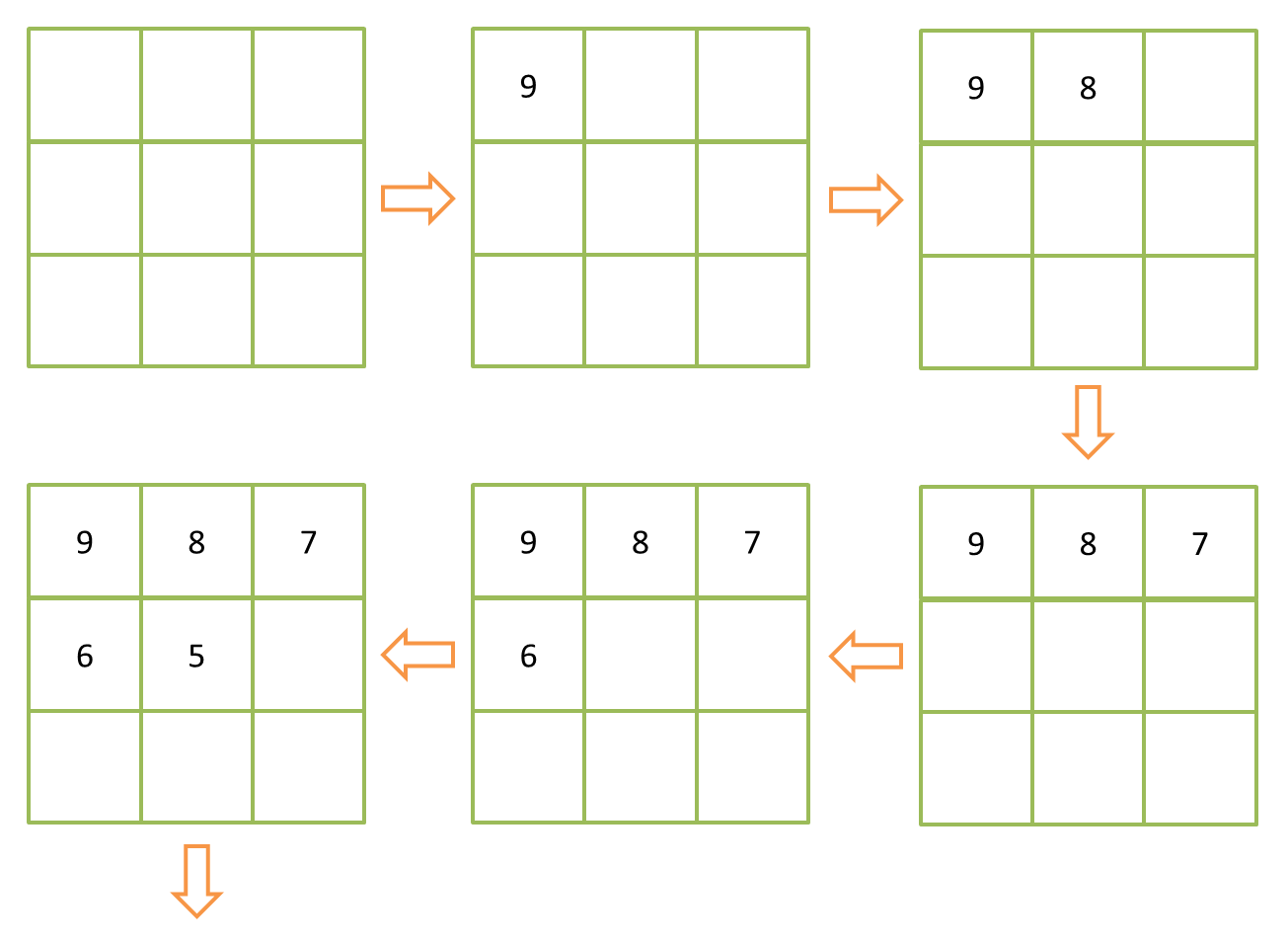
代碼如下:
int g_cnt = 0;
void FillBlank(int num)
{
int i;
int nBak;
int* pArr = (int*)g_arr;
if (num <= 0)
{
if (Calculate() == 1)
{
PrintMap();
}
printf("%d\r", g_cnt++);
return;
}
for (i = 0; i < MAX_SIZE * MAX_SIZE; i++)
{
if (num >= pArr[i])
{
nBak = pArr[i];
pArr[i] = num;
FillBlank(num - 1);
pArr[i] = nBak;
}
}
}
函數(shù)FillBlank()的功能是把數(shù)字num填在一個(gè)空格中犹赖。每一層遞歸函數(shù)調(diào)用下一層函數(shù)時(shí),傳遞一個(gè)num - 1卷仑。當(dāng)參數(shù)為0時(shí)峻村,說明這個(gè)分支到達(dá)最低端的葉子節(jié)點(diǎn)。這時(shí)候二位數(shù)組中保存的是一個(gè)完成的可能锡凝。通過Caculate()函數(shù)判斷它是否符合題意粘昨,如果符合就打印出來。這里打印的是所有符合題意的可能。
在FillBlank()中张肾,我們通過一個(gè)循環(huán)遍歷九個(gè)空格芭析,當(dāng)要填寫的數(shù)字大于格子中的數(shù)字時(shí),說明可以填寫吞瞪。這樣就保證了每一層的填寫次數(shù)正確馁启。
最后,在填寫數(shù)字之前芍秆,需要先用nBak變量保存空格中原有的數(shù)字惯疙,在這一輪遞歸結(jié)束后要恢復(fù)回來。原因大家好好思考一下妖啥。
注意:由于窮舉的次數(shù)太多霉颠,等待的過程會(huì)比較漫長(zhǎng),我們?cè)谶@里加入了一個(gè)顯示當(dāng)前尋找次數(shù)的功能荆虱。全局變量g_cnt記錄了找到的可能性次數(shù)蒿偎,通過printf("%d\r", g_cnt++);不斷打印在屏幕上。
6. 功能調(diào)用
main()函數(shù)變得非常簡(jiǎn)單:
int main()
{
FillBlank(9);
return 0;
}
我們執(zhí)行一下怀读,效果如下:

7. 留下一種結(jié)果
對(duì)現(xiàn)有的程序稍作修改诉位,我們只需要一個(gè)符合題意的結(jié)果即可。代碼如下:
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#define MAX_SIZE 3
int g_arr[MAX_SIZE][MAX_SIZE] = { 0 };
int Calculate()
{
int i, j;
int sumLine, sumCol, sumDL1, sumDL2;
sumDL1 = 0;
sumDL2 = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sumLine = 0;
sumCol = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sumLine += g_arr[i][j];
sumCol += g_arr[j][i];
}
if (sumLine != 15 || sumCol != 15)
{
return 0;
}
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE - 1 - i];
}
if (sumDL1 != 15 || sumDL2 != 15)
{
return 0;
}
return 1;
}
void PrintMap()
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d ", g_arr[i][j]);
}
printf("\n");
}
printf("\n");
}
int g_cnt = 0;
int g_return = 0;
void FillBlank(int num)
{
int i;
int nBak;
int* pArr = (int*)g_arr;
if (g_return == 1)
{
return;
}
if (num <= 0)
{
if (Calculate() == 1)
{
PrintMap();
g_return = 1;
}
printf("%d\r", g_cnt++);
return;
}
for (i = 0; i < MAX_SIZE * MAX_SIZE; i++)
{
if (num >= pArr[i])
{
nBak = pArr[i];
pArr[i] = num;
FillBlank(num - 1);
pArr[i] = nBak;
}
}
}
int main()
{
FillBlank(9);
return 0;
}
執(zhí)行效果如下:

由于這個(gè)遞歸方法比較抽象菜枷,不理解的同學(xué)可以在群里提問不从,我再仔細(xì)講解一下。
8. 課后練習(xí)
給出一組代數(shù)表達(dá)式犁跪,請(qǐng)編程判斷出他們的括號(hào)是否配對(duì)正確。
8.1 輸入內(nèi)容
5
[a+(b+c)]*(a+b]
(a-1+b)-(b+c)
x-[a*(b+c))]
a+(b+c+(d-(e+m))
a+b+[c-d*e-(a-b)-c]
第一行中的5表示共有5個(gè)表達(dá)式需要判斷歹袁。下面的每一行有一個(gè)表達(dá)式坷衍。要求把這組數(shù)據(jù)原樣保存在文件input.txt中,通過讀文件的方式讀入數(shù)據(jù)完成判斷条舔。
8.2 輸出
括號(hào)匹配正確打印1枫耳,匹配錯(cuò)誤打印0。正確的輸出結(jié)果應(yīng)該是:
0
1
0
0
1
我是天花板孟抗,讓我們一起在軟件開發(fā)中自我迭代迁杨。
如有任何問題,歡迎與我聯(lián)系凄硼。