上一篇的迷宮問題難倒了很多人桐猬,對于初學者這個相對綜合的問題可能的確有點難麦撵,不過并非完成不了。我們今天就來看看初學者如何用最基礎的方法解決這個問題溃肪。
1. 題目

如圖所示免胃,有一個6 * 6的迷宮,左上角為入口惫撰,右下角為出口羔沙。圖中0的位置可以走,1的位置不能走厨钻。請編程找出唯一的一條通過迷宮的路扼雏。
2. 分析
2.1 經典解法
這道題是一個C語言編程中的經典題目坚嗜,網上的答案有很多。有人還真去查了诗充,但結果有點崩潰苍蔬,他們看到的是:回溯、遞歸蝴蜓、堆棧碟绑、迭代、DFS這些初學者根本沒怎么聽過的關鍵詞茎匠。那些沒有注釋的例程也是怎么也看不懂格仲。其實,就因為題目太過經典诵冒,所以才有各種五花八門的解法抓狭。
總結一下,主流的解法就兩種:
- DFS 深度優(yōu)先遍歷法
通過遞歸的方式不斷從入口尋找下一個可行的點造烁,依次執(zhí)行下去。一旦發(fā)現死路就退回到上一個點重新尋找新路線午笛。
理論上遍歷了所有可能的路線之后惭蟋,正確的路線一定能夠找到。
- BFS 廣度優(yōu)先遍歷法
這個算法的特點是不需要遞歸药磺,需要自己維護一個順序表告组,之后通過循環(huán)同時尋找和當前點相連的每一個聯通的點,直到找到出口癌佩。
這個算法的特點是不需要回退木缝。
以上兩種是數據結構中的經典算法,不過我們今天要講的并非這兩種围辙。所以千萬不要被嚇到了我碟。
2.2 功能分解
首先說一下,經典的編程問題姚建,每個都有經典的解法矫俺。這些解法是很多人共同總結出來的可以解決一類問題的最優(yōu)算法。然而掸冤,對于某一個具體的問題厘托,這些算法并不一定是最優(yōu)的或者說最簡單的。
這道題就是這樣稿湿。迷宮問題最大的難點就是它有很多岔路是走不通的铅匹。那我們想想,如果迷宮沒有岔路你會做嗎饺藤?

相信大部分人都能解決包斑。那么這就是我們的目標流礁。
- 功能一:迷宮打印
把迷宮打印在屏幕上,其實是二維數組的打印舰始。
- 功能二:迷宮剪支
把迷宮中所有的死路刪除崇棠。
- 功能三:標記正確路線
最后我們需要把正確的路線打印在屏幕中。
從步驟上說丸卷,我們要做的就是這三件事枕稀。要把大象放冰箱,總共分幾步谜嫉,分三步萎坷。
3. 代碼框架
依然是堆積木,我們今天先寫main函數的框架沐兰,之后把積木填進去哆档。
void main()
{
int i, j, k;
int maze[MAX_SIZE][MAX_SIZE] =
{
{ 0, 1, 0, 1, 1, 1 },
{ 0, 0, 0, 1, 0, 1 },
{ 0, 1, 1, 0, 0, 0 },
{ 0, 1, 1, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 1, 1, 1, 1, 0 }
};
// 打印原始迷宮
printf("原始迷宮:\n");
// 迷宮剪支
// 打印剪支后的迷宮
printf("\n剪支后的迷宮:\n");
// 打印帶正確路線的迷宮
printf("\n標記迷宮路線:\n");
}
這里我多加了一部分“打印剪支后的迷宮”,為了讓大家可以看到中間過程住闯,方便調試瓜浸。
4. 打印迷宮
這就是一個普通的二維數組打印,代碼如下:
void PrintMaze(int arrMaze[][MAX_SIZE])
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d", arrMaze[i][j]);
}
printf("\n");
}
}
5. 迷宮剪支
5.1 空間復制
由于我們做剪支時會修改二維數組的內容比原,為了保持原始數組不被破壞插佛,我們要先復制出一個新的二維數組。復制函數如下:
void Copy(int* pDest, int* pSrc, int cnt)
{
while (cnt--)
{
*pDest++ = *pSrc++;
}
}
這幾乎是課本上的例子程序量窘,應該不用多介紹了雇寇。沒學過指針的同學可以用數組的方法來實現。這里又涉及到二維數組的空間當一維數組來使用蚌铜。
接下來锨侯,我們就可以在一塊復制出來的迷宮里做任何想要的操作了。
5.2 剪支
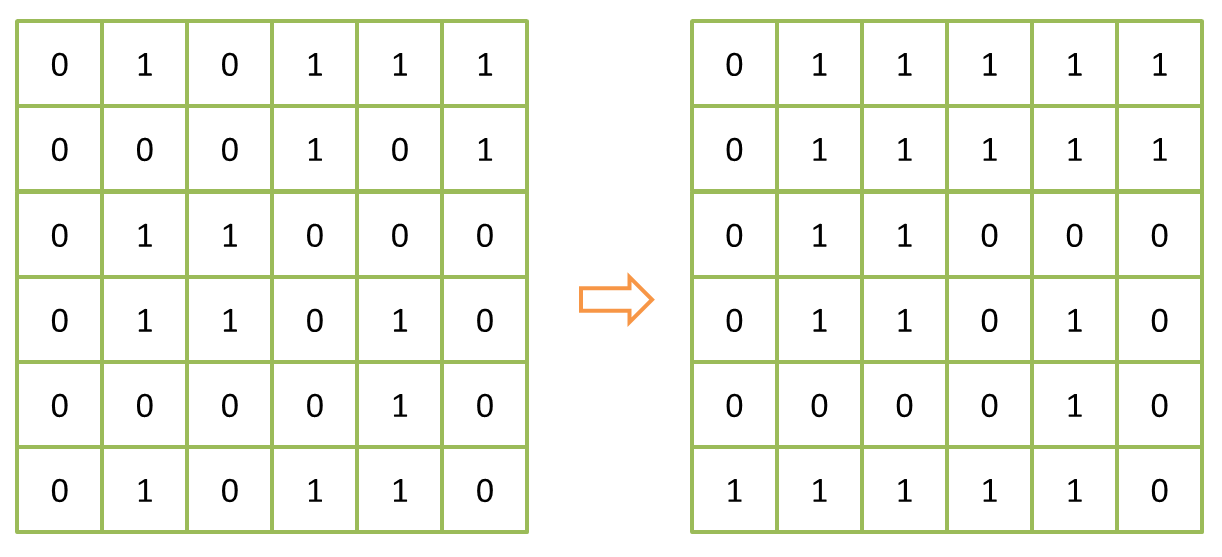
如圖所示冬殃,我們的目標就是把左邊這個二維數組轉換成右邊這個二維數組囚痴。
算法很簡單,遍歷二維數組造壮,找到上下左右四個位置中只有一個或根本沒有0的位置渡讼,如果它是0則改為1。
用人話說就是找到每條死路的最后一個位置耳璧,把它變成1成箫。這樣循環(huán)下去就能夠將整條死路徹底封死。如下圖:
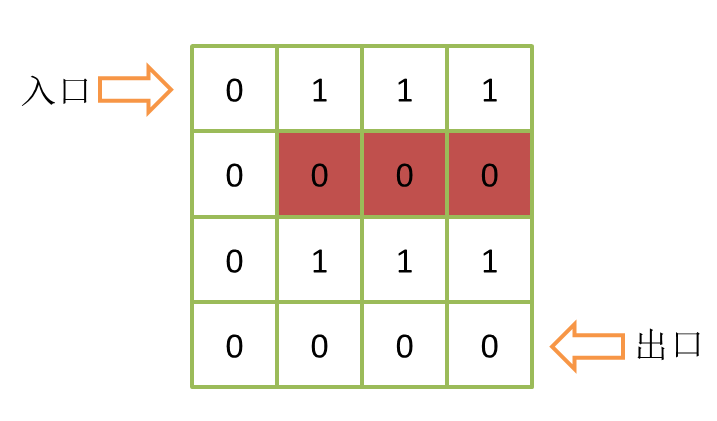
圖中紅色部分是一條死路旨枯,但我們遍歷一遍只能把最右邊的紅色位置寫入1蹬昌,此時死路的盡頭變成了中間這個紅色方塊。我們還需要繼續(xù)循環(huán)攀隔,但這種死路有幾個長度就循環(huán)幾次的方式顯然不是最優(yōu)解皂贩。因此我們要設計一個算法能夠一次就封死整個路徑栖榨。
代碼如下:
int CountPath(int maze[][MAX_SIZE], int i, int j)
{
int cnt = 0;
// Up Point
if (i > 0)
{
if (maze[i - 1][j] == 0 || maze[i - 1][j] == 2)
{
cnt++;
}
}
// Down Point
if (i < MAX_SIZE - 1)
{
if (maze[i + 1][j] == 0 || maze[i + 1][j] == 2)
{
cnt++;
}
}
// Left Point
if (j > 0)
{
if (maze[i][j - 1] == 0 || maze[i][j - 1] == 2)
{
cnt++;
}
}
// Right Point
if (j < MAX_SIZE - 1)
{
if (maze[i][j + 1] == 0 || maze[i][j + 1] == 2)
{
cnt++;
}
}
return cnt;
}
void FindNext(int maze[][MAX_SIZE], int i, int j)
{
int cnt;
int line, colum;
// Up Point
if (i > 0)
{
line = i - 1;
colum = j;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Down Point
if (i < MAX_SIZE - 1)
{
line = i + 1;
colum = j;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Left Point
if (j > 0)
{
line = i;
colum = j - 1;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Right Point
if (j < MAX_SIZE - 1)
{
line = i;
colum = j + 1;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
}
void CutBranch(int arrMaze[][MAX_SIZE])
{
int i, j;
arrMaze[0][0] = 2; // entry
arrMaze[MAX_SIZE - 1][MAX_SIZE - 1] = 2; // exit
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
if (arrMaze[i][j] != 0)
{
continue;
}
if (CountPath(arrMaze, i, j) <= 1)
{
arrMaze[i][j] = 1;
FindNext(arrMaze, i, j);
}
}
}
}
我們通過調用CutBranch()函數來遍歷每一個位置。注意明刷,這里只做了一次遍歷婴栽。
當某個位置是0時,調用CountPath()函數計算出它的周圍有幾個0辈末。如果是0個或1個愚争,說明它是死路,修改它的值為1之后再調用FindNext()函數判斷它周圍的位置挤聘。
重點說一下轰枝,FindNext()函數,它的參數是一個二維數組和一組i,j表示的位置组去。功能是判斷這個位置上下左右四個位置是否為死路鞍陨,如果是就修改成1之后再調用FindNext()尋找修改之后它周圍是否存在死路的情況。
注意:
- 在FindNext()中首先要判斷是否在迷宮邊上从隆,否則直接訪問可能會造成數組越界
- 由于入口和出口兩個位置也滿足死路的條件诚撵,因此我們在CutBranch()中把它們置為2
CutBranch()函數執(zhí)行完后,我們就得到了一個只有一條正確路線的迷宮键闺。
6. 標記路線
最后砾脑,把我們得到這條路徑在原迷宮中標記出來。我們用9表示正確的路線艾杏。
void MarkMaze(int srcMaze[][MAX_SIZE], int markMaze[][MAX_SIZE])
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
if (markMaze[i][j] == 0)
{
srcMaze[i][j] = 9;
}
}
}
}
遍歷markMaze,發(fā)現0就在srcMaze相應的位置上寫9。
最后我們看看main函數中的函數調用:
void main()
{
int i, j, k;
int maze[MAX_SIZE][MAX_SIZE] =
{
{ 0, 1, 0, 1, 1, 1 },
{ 0, 0, 0, 1, 0, 1 },
{ 0, 1, 1, 0, 0, 0 },
{ 0, 1, 1, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 1, 1, 1, 1, 0 }
};
int mazeCpy[MAX_SIZE][MAX_SIZE];
// 打印原始迷宮
printf("原始迷宮:\n");
PrintMaze(maze);
// 迷宮剪支
Copy((int*)mazeCpy, (int*)maze, MAX_SIZE * MAX_SIZE);
CutBranch(mazeCpy);
// 打印剪支后的迷宮
printf("\n剪支后的迷宮:\n");
PrintMaze(mazeCpy);
// 打印帶正確路線的迷宮
MarkMaze(maze, mazeCpy);
printf("\n標記迷宮路線:\n");
PrintMaze(maze);
}
看看最后的執(zhí)行結果:
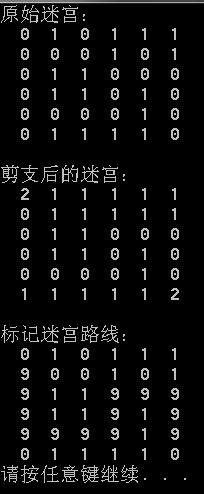
7. 總結
這個算法是不是沒有用到任何大家沒學過的知識呢盅藻。先把我當代碼看懂购桑,之后考慮下面兩個問題:
- 這個算法找到的路線是否一定是最短的路線呢?
- 判斷每個位置是否在迷宮邊上非常麻煩氏淑,有沒有什么好辦法簡化這個操作呢勃蜘?
請大家仔細思考這兩個問題,我會在群里公布優(yōu)化后的代碼假残。
8. 課后作業(yè)

把一個硬幣拋5次缭贡,打印出所有可能出現的情況。1表示正面辉懒,0表示背面阳惹。比如:
全正面
1 1 1 1 1
全背面
0 0 0 0 0
我是天花板,讓我們一起在軟件開發(fā)中自我迭代眶俩。
如有任何問題莹汤,歡迎與我聯系。