引論
我自己的房間一直很混亂,偶爾清理整潔潘悼,不過幾天,便又回歸混亂治唤。想來當似熱力學(xué)中的「熵增原理」。
然而耗散系統(tǒng)卻可以自然的形成某種「形式」船惨,赫爾曼·哈肯在《協(xié)同學(xué)》中介紹了一個現(xiàn)象:用適當?shù)姆绞郊訜嵋后w缕陕,液體會形成穩(wěn)定的、周期性的形狀扛邑。即它自發(fā)的形成了某種秩序。
但整理房間恶座、整理物件沥阳,最要緊的便是「簡單」跨琳,復(fù)雜的方法總難堅持。而基于啟發(fā)式策略的「生命游戲」則足夠簡單桐罕,也可以形成某種秩序,可以試著用它來整理房間功炮。
Game of Life
所謂「生命游戲」(Game of Life),就如下圖所示伟恶,是在一個棋盤之中毅该,有黑色的點,有白色的點眶掌。黑色代表這里有一個點,通過簡單的規(guī)則即寒,產(chǎn)生豐富的圖樣。
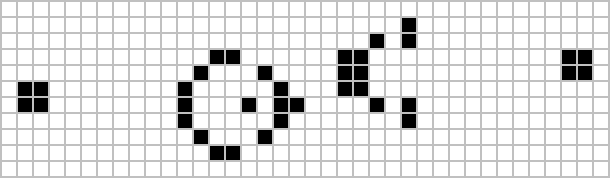
它的基本規(guī)則是:
- 當一個點周圍的點的數(shù)量高于某數(shù)時逸爵,它將因為太擁擠而死亡凹嘲;
- 當小于某數(shù)時,將因為太孤獨而死亡周蹭。
- 當某空白點周圍的黑子數(shù)目符合某條件時,將會產(chǎn)生出一個新的點瓷胧。

通過這種簡單的過程棚愤,可以形成非常非常復(fù)雜而有序的結(jié)構(gòu),比如上圖,是一個周期結(jié)構(gòu)耍休,穩(wěn)定的放在那里。
這與我們收拾房間在某些方面是相似的斯够。
- 房間內(nèi)的物體不可以太過擁擠喧锦,太擁擠則難以取用;
- 房間內(nèi)的物體不可太過零散燃少,太零散則雜亂無章;
基于上邊兩條「基本法」碍遍,可以構(gòu)建一個自動機模型阳液。不過這里與生命游戲有一點差別:
房間里的東西不會無故丟失,也不會無故產(chǎn)生
也就是說帘皿,過于擁擠、零散的點上的物體虽填,要改換位置,這個變換的方式當有所講究涩惑,即優(yōu)先放到與自己類型相同的物體旁邊桑驱。
注意到這個時候,我們所有的規(guī)則都是基于單個點的熬的,這是這種策略的一個優(yōu)勢:即我們在收拾房間的時候,只需要考慮有限的物體岔绸。
代碼模擬
我們使用Mathematica建模模擬橡伞,下面是對代碼的一些解釋:
建立隨機初始值:

這段代碼是用來初始化和建立地圖的,其中:
randM = map*
Table[RandomChoice[{1, 1, 3} -> {1, 2, 0}], {i, 1, 40}, {j, 1,
40}];
用map矩陣數(shù)乘隨機產(chǎn)生的矩陣刚盈,用來使其符合地圖之要求挂脑。
隨機選取點進行處理,并依照一定規(guī)則移動細胞:
PRandom[m_, mx_] :=(*根據(jù)mx矩陣的高斯卷積產(chǎn)生加權(quán)隨機數(shù)肋联,決定與之交換的點*)
Module[{pm = GaussianFilter[m, 2], wlist = {}, elist = {}},
pm = Table[
If[mx[[i]][[j]] == 0 && map[[i]][[j]] == 1, pm[[i]][[j]], 0], {i,
1, Length[m]}, {j, 1, Length[m[[1]]]}];
wlist = Flatten[pm];
elist =
Flatten[Table[{x, y}, {x, 1, Length[m]}, {y, 1, Length[m[[1]]]}],
1];
RandomChoice[wlist*wlist -> elist]
]
m是某顏色物體的矩陣刁俭,mx是各個顏色物體的矩陣,其中pm是對m的高斯核卷積牍戚,以此算出隨機座標的權(quán)值。PRandom[]函數(shù)本身就是依照m與mx矩陣給出一個隨機座標鼎天,從而決定當前點移動到哪一點暑竟。
PRandomN[m_, n_] :=
(*對顏色為n的點進行操作*)
Module[{m2 =
Table[If[m[[i]][[j]] == n, 1, 0], {i, 1, Length[m]}, {j, 1,
Length[m[[1]]]}]}, PRandom[m2, m]]
PRandom則是依照顏色n給出隨機座標育勺。
選取一點周圍的八個點:
TakeAroundList[list_, p_] := Module[{len = Length[list]},
Which[
1 < p < len, list[[p - 1 ;; p + 1]],
p == 1, {list[[len]]}~Join~list[[1 ;; 2]],
p == len, list[[len - 1 ;; len]]~Join~{list[[1]]}
]
]
TakeAround[m_, {x_, y_}] :=
Transpose@TakeAroundList[Transpose@TakeAroundList[m, x], y]
這兩段代碼比較簡單罗岖,不做詳細敘述,功能就是給出某一座標x,y周圍的八個點(考慮了邊緣部分的問題)南蓬。
隨機增減物體:
PutInAndDelet[m_, {p1_, p2_}] :=
Module[{m2 = m, pm = (1 - Sign /@ m)*map, wlist = {}, elist = {},
x = 1, y = 1, maxColor = Max[m], pm2 = {}, xd = 1, yd = 1},
pm2 = (1 - pm)*map;
wlist = Flatten[pm];
elist =
Flatten[Table[{x, y}, {x, 1, Length[m]}, {y, 1, Length[m[[1]]]}],
1];
{x, y} = RandomChoice[wlist -> elist];
{xd, yd} = RandomChoice[Flatten[pm2] -> elist];
If[RandomReal[] < p1, m2[[x]][[y]] = RandomInteger[{1, maxColor}]];
If[RandomReal[] < p1, m2[[xd]][[yd]] = 0];
m2
]
隨機向內(nèi)撒入物體哑了,隨機模式依照先前的PRandom[]思想。
迭代一次:
ChangeOne[m_] :=
Module[{m2 = m, a = Length[m], b = Length[m[[1]]],
x = RandomInteger[{1, Length[m]}],
y = RandomInteger[{1, Length[m[[1]]]}], MRound = {}, MRound01 = {},
n1 = 0, n2 = 0, p = 4, px = 0, py = 0},(*x,y隨機生成窄陡,作為迭代對象的座標*)
If[m[[x]][[y]] != 0,(*某點是物體的時候拆火,執(zhí)行下述操作*)
MRound = TakeAround[m, {x, y}];
MRound[[2]][[2]] = 0;
MRound01 = Sign /@ MRound;
n1 = Total[Flatten[MRound01]];(*以上操作給出其周圍鄰居數(shù)量*)
{px, py} = PRandomN[m, m[[x]][[y]]];(*隨機給出移動方位*)
If[
n1 != p, m2[[px]][[py]] = m[[x]][[y]]; m2[[x]][[y]] = 0(*若不符合宜居條件,則移動*)
]; m2,
ChangeOne[m](*若此點為空币叹,則遞歸直到此點非空*)
]
]
ChangeOne[]代表迭代一次模狭,輸入為一矩陣,輸出亦為一矩陣胞皱。為了效率九妈,地圖數(shù)據(jù)使用全局變量。注釋見代碼宴树。
有了ChangeOne[]函數(shù)之后晶疼,便可以使用Nest[]和NestList[]函數(shù)對其進行迭代。
實際迭代實驗:
mxList = NestList[Nest[ChangeOne, #, 1000] &, randM, 5];
Table[ArrayPlot[mxList[[i]], ColorFunction -> "Rainbow",
Epilog -> {Polygon[{{0, 40}, {11, 40}, {11, 29}, {0, 29}}],
Polygon[{{18, 0}, {18, 12}, {40, 12}, {40, 0}}]}], {i, 1, 6}]
給出如下圖像:

可以看到其由隨機锭吨、混亂的狀態(tài)漸漸的變得有序寒匙。
我們還可以考察它的聚合度,聚合度定義為Count[Flatten[mr], mr[[2]][[2]]]/8,其越接近于1則越密集祸憋。下面是隨著系統(tǒng)演化肖卧,聚合度變化的過程:

可以明顯的看到,其聚合度很快便上升到了約0.7左右(多次實驗都穩(wěn)定在這個值)拦赠。并且這個圖是考慮了隨機增減物品后的圖像壁榕,其對隨機增加的物品的承受力比較強。
當然牌里,我自己也要在實際生活中實踐這個啟發(fā)式策略,看看是否能產(chǎn)生效用喳篇。