第十三章 二叉搜索樹

原文：Chapter 13 Binary search tree

譯者：飛龍

協(xié)議：CC BY-NC-SA 4.0

自豪地采用谷歌翻譯

本章介紹了上一個練習(xí)的解決方案卧檐，然后測試樹形映射的性能捕仔。我展示了一個實現(xiàn)的問題钓葫，并解釋了 Java 的TreeMap如何解決它础浮。

13.1 簡單的MyTreeMap

上一個練習(xí)中，我給了你MyTreeMap的大綱鸭廷，并讓你填充缺失的方法》鹣牛現(xiàn)在我會展示結(jié)果宵晚，從findNode開始：

private Node findNode(Object target) {
    // some implementations can handle null as a key, but not this one
    if (target == null) {
            throw new IllegalArgumentException();
    }

    // something to make the compiler happy
    @SuppressWarnings("unchecked")
    Comparable<? super K> k = (Comparable<? super K>) target;

    // the actual search
    Node node = root;
    while (node != null) {
        int cmp = k.compareTo(node.key);
        if (cmp < 0)
            node = node.left;
        else if (cmp > 0)
            node = node.right;
        else
            return node;
    }
    return null;
}

findNode是containsKey和get所使用的一個私有方法；它不是Map接口的一部分维雇。參數(shù)target是我們要查找的鍵。我在上一個練習(xí)中解釋了這種方法的第一部分：

• 在這個實現(xiàn)中晒他，null不是鍵的合法值吱型。
• 在我們可以在target上調(diào)用compareTo之前，我們必須把它強制轉(zhuǎn)換為某種形式的Comparable陨仅。這里使用的“類型通配符”會盡可能允許津滞；也就是說，它適用于任何實現(xiàn)Comparable類型灼伤，并且它的compareTo接受K或者任和K的超類触徐。

之后，實際搜索比較簡單狐赡。我們初始化一個循環(huán)變量node來引用根節(jié)點撞鹉。每次循環(huán)中，我們將目標與node.key比較。如果目標小于當(dāng)前鍵鸟雏，我們移動到左子樹享郊。如果它更大，我們移動到右子樹孝鹊。如果相等炊琉，我們返回當(dāng)前節(jié)點。

如果在沒有找到目標的情況下又活，我們到達樹的底部苔咪，我就認為，它不在樹中并返回null柳骄。

13.2 搜索值

我在前面的練習(xí)中解釋了悼泌，findNode運行時間與樹的高度成正比，而不是節(jié)點的數(shù)量夹界，因為我們不必搜索整個樹馆里。但是對于containsValue，我們必須搜索值可柿，而不是鍵鸠踪；BST 的特性不適用于值，因此我們必須搜索整個樹复斥。

我的解法是遞歸的：

public boolean containsValue(Object target) {
    return containsValueHelper(root, target);
}

private boolean containsValueHelper(Node node, Object target) {
    if (node == null) {
        return false;
    }
    if (equals(target, node.value)) {
        return true;
    }
    if (containsValueHelper(node.left, target)) {
        return true;
    }
    if (containsValueHelper(node.right, target)) {
        return true;
    }
    return false;
}

containsValue將目標值作為參數(shù)营密，并立即調(diào)用containsValueHelper，傳遞樹的根節(jié)點作為附加參數(shù)目锭。

這是containsValueHelper的工作原理：

• 第一個if語句檢查遞歸的邊界情況评汰。如果node是null，那意味著我們已經(jīng)遞歸到樹的底部痢虹，沒有找到target被去，所以我們應(yīng)該返回false。請注意奖唯，這只意味著目標沒有出現(xiàn)在樹的一條路徑上惨缆；它仍然可能會在另一條路徑上被發(fā)現(xiàn)。
• 第二種情況檢查我們是否找到了我們正在尋找的東西丰捷。如果是這樣坯墨，我們返回true。否則病往，我們必須繼續(xù)捣染。
• 第三種情況是執(zhí)行遞歸調(diào)用，在左子樹中搜索target停巷。如果我們找到它耍攘，我們可以立即返回true榕栏，而不搜索右子樹。否則我們繼續(xù)少漆。
• 第四種情況是搜索右子樹臼膏。同樣，如果我們找到我們正在尋找的東西示损，我們返回true渗磅。否則，我們搜索完了整棵樹检访，返回false始鱼。

該方法“訪問”了樹中的每個節(jié)點，所以它的所需時間與節(jié)點數(shù)成正比脆贵。

13.3 實現(xiàn)put

put方法比起get要復(fù)雜一些医清，因為要處理兩種情況：（1）如果給定的鍵已經(jīng)在樹中，則替換并返回舊值卖氨；（2）否則必須在樹中添加一個新的節(jié)點会烙，在正確的地方。

在上一個練習(xí)中筒捺，我提供了這個起始代碼：

public V put(K key, V value) {
    if (key == null) {
        throw new IllegalArgumentException();
    }
    if (root == null) {
        root = new Node(key, value);
        size++;
        return null;
    }
    return putHelper(root, key, value);
}

并且讓你填充putHelper柏腻。這里是我的答案：

private V putHelper(Node node, K key, V value) {
    Comparable<? super K> k = (Comparable<? super K>) key;
    int cmp = k.compareTo(node.key);

    if (cmp < 0) {
        if (node.left == null) {
            node.left = new Node(key, value);
            size++;
            return null;
        } else {
            return putHelper(node.left, key, value);
        }
    }
    if (cmp > 0) {
        if (node.right == null) {
            node.right = new Node(key, value);
            size++;
            return null;
        } else {
            return putHelper(node.right, key, value);
        }
    }
    V oldValue = node.value;
    node.value = value;
    return oldValue;
}

第一個參數(shù)node最初是樹的根，但是每次我們執(zhí)行遞歸調(diào)用系吭，它指向了不同的子樹五嫂。就像get一樣，我們用compareTo方法來弄清楚肯尺，跟隨哪一條樹的路徑沃缘。如果cmp < 0，我們添加的鍵小于node.key则吟，那么我們要走左子樹槐臀。有兩種情況：

• 如果左子樹為空，那就是逾滥，如果node.left是null峰档，我們已經(jīng)到達樹的底部而沒有找到key。這個時候寨昙，我們知道key不在樹上，我們知道它應(yīng)該放在哪里掀亩。所以我們創(chuàng)建一個新節(jié)點舔哪，并將它添加為node的左子樹。
• 否則我們進行遞歸調(diào)用來搜索左子樹槽棍。

如果cmp > 0捉蚤，我們添加的鍵大于node.key抬驴，那么我們要走右子樹。我們處理的兩個案例與上一個分支相同缆巧。最后布持，如果cmp == 0，我們在樹中找到了鍵陕悬，那么我們更改它并返回舊的值题暖。

我使用遞歸編寫了這個方法，使它更易于閱讀捉超，但它可以直接用迭代重寫一遍胧卤，你可能想留作練習(xí)。

13.4 中序遍歷

我要求你編寫的最后一個方法是keySet拼岳，它返回一個Set枝誊，按升序包含樹中的鍵。在其他Map實現(xiàn)中惜纸，keySet返回的鍵沒有特定的順序叶撒，但是樹形實現(xiàn)的一個功能是，對鍵進行簡單而有效的排序耐版。所以我們應(yīng)該利用它祠够。

這是我的答案：

public Set<K> keySet() {
    Set<K> set = new LinkedHashSet<K>();
    addInOrder(root, set);
    return set;
}

private void addInOrder(Node node, Set<K> set) {
    if (node == null) return;
    addInOrder(node.left, set);
    set.add(node.key);
    addInOrder(node.right, set);        
}

在keySet中，我們創(chuàng)建一個LinkedHashSet椭更，這是一個Set實現(xiàn)哪审，使元素保持有序（與大多數(shù)其他Set實現(xiàn)不同）。然后我們調(diào)用addInOrder來遍歷樹虑瀑。

第一個參數(shù)node最初是樹的根湿滓，但正如你的期望，我們用它來遞歸地遍歷樹舌狗。addInOrder對樹執(zhí)行經(jīng)典的“中序遍歷”叽奥。

如果node是null，這意味著子樹是空的痛侍，所以我們返回朝氓，而不向set添加任何東西。否則我們：

1. 按順序遍歷左子樹主届。
2. 添加node.key赵哲。
3. 按順序遍歷右子樹。

請記住君丁，BST 的特性保證左子樹中的所有節(jié)點都小于node.key枫夺，并且右子樹中的所有節(jié)點都更大。所以我們知道绘闷，node.key已按正確的順序添加橡庞。

遞歸地應(yīng)用相同的參數(shù)较坛，我們知道左子樹中的元素是有序的，右子樹中的元素也一樣扒最。并且邊界情況是正確的：如果子樹為空丑勤，則不添加任何鍵。所以我們可以認為吧趣，該方法以正確的順序添加所有鍵法竞。

因為containsValue方法訪問樹中的每個節(jié)點，所以所需時間與n成正比再菊。

13.5 對數(shù)時間的方法

在MyTreeMap中爪喘，get和put方法所需時間與樹的高度h成正比。在上一個練習(xí)中纠拔，我們展示了如果樹是滿的 - 如果樹的每一層都包含最大數(shù)量的節(jié)點 - 樹的高度與log n成橫臂秉剑。

我也說了，get和put是對數(shù)時間的稠诲；也就是說侦鹏，他們的所需時間與logn成正比。但是對于大多數(shù)應(yīng)用程序臀叙，不能保證樹是滿的略水。一般來說，樹的形狀取決于鍵和添加順序劝萤。

為了看看這在實踐中是怎么回事渊涝，我們將用兩個樣本數(shù)據(jù)集來測試我們的實現(xiàn)：隨機字符串的列表和升序的時間戳列表。

這是生成隨機字符串的代碼：

Map<String, Integer> map = new MyTreeMap<String, Integer>();

for (int i=0; i<n; i++) {
    String uuid = UUID.randomUUID().toString();
    map.put(uuid, 0);
}

UUID是java.util中的類床嫌，可以生成隨機的“通用唯一標識符”跨释。UUID 對于各種應(yīng)用是有用的，但在這個例子中厌处，我們利用一種簡單的方法來生成隨機字符串鳖谈。

我使用n=16384來運行這個代碼，并測量了最后的樹的運行時間和高度阔涉。以下是輸出：

Time in milliseconds = 151
Final size of MyTreeMap = 16384
log base 2 of size of MyTreeMap = 14.0
Final height of MyTreeMap = 33

我包含了“MyTreeMap大小的2為底的對數(shù)”缆娃，看看如果它已滿，樹將是多高瑰排。結(jié)果表明贯要，高度為14的完整樹包含16384個節(jié)點。

隨機字符串的樹高度實際為33椭住，這遠大于理論上的最小值郭毕，但不是太差。要查找16,384個鍵中的一個函荣，我們只需要進行33次比較显押。與線性搜索相比，速度快了近500倍傻挂。

這種性能通常是隨機字符串乘碑，或其他不按照特定順序添加的鍵。樹的最終高度可能是理論最小值的2~3倍金拒，但它仍然與log n成正比兽肤，這遠小于n。事實上绪抛，隨著n的增加资铡，logn會慢慢增加，在實踐中幢码，可能很難將對數(shù)時間與常數(shù)時間區(qū)分開笤休。

然而，二叉搜索樹并不總是表現(xiàn)良好症副。讓我們看看店雅，當(dāng)我們以升序添加鍵時會發(fā)生什么。下面是一個示例贞铣，以微秒為單位測量時間戳闹啦，并將其用作鍵：

MyTreeMap<String, Integer> map = new MyTreeMap<String, Integer>();

for (int i=0; i<n; i++) {
    String timestamp = Long.toString(System.nanoTime());
    map.put(timestamp, 0);
}

System.nanoTime返回一個long類型的整數(shù)，表示以微秒為單位的啟動時間辕坝。每次我們調(diào)用它時窍奋，我們得到一個更大的數(shù)字。當(dāng)我們將這些時間戳轉(zhuǎn)換為字符串時酱畅，它們按字典序增加琳袄。

讓我們看看當(dāng)我們運行它時會發(fā)生什么：

Time in milliseconds = 1158
Final size of MyTreeMap = 16384
log base 2 of size of MyTreeMap = 14.0
Final height of MyTreeMap = 16384

運行時間是以前的時間的七倍多。時間更長圣贸。如果你想知道為什么挚歧，看看樹的最后的高度：16384！

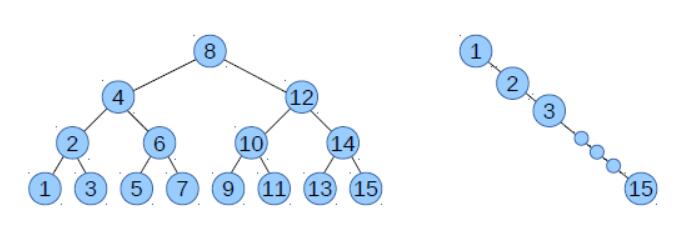
圖 13.1：二叉搜索樹吁峻，平衡（左邊）和不平衡（右邊）

如果你思考put如何工作滑负，你可以弄清楚發(fā)生了什么。每次添加一個新的鍵時用含，它都大于樹中的所有鍵矮慕，所以我們總是選擇右子樹，并且總是將新節(jié)點添加為啄骇，最右邊的節(jié)點的右子節(jié)點痴鳄。結(jié)果是一個“不平衡”的樹，只包含右子節(jié)點缸夹。

這種樹的高度正比于n痪寻，不是logn螺句，所以get和put的性能是線性的，不是對數(shù)的橡类。

圖 13.1 顯示了平衡和不平衡樹的示例蛇尚。在平衡樹中，高度為4顾画，節(jié)點總數(shù)為2^4 - 1 = 15取劫。在節(jié)點數(shù)相同的不平衡樹中，高度為15研侣。

13.6 自平衡樹

這個問題有兩種可能的解決方案：

你可以避免向Map按順序添加鍵谱邪。但這并不總是可能的。
你可以制作一棵樹庶诡，如果碰巧按順序處理鍵惦银，那么它會更好地處理鍵。

第二個解決方案是更好的灌砖，有幾種方法可以做到璧函。最常見的是修改put，以便它檢測樹何時開始變得不平衡基显，如果是蘸吓，則重新排列節(jié)點。具有這種能力的樹被稱為“自平衡樹”撩幽。普通的自平衡樹包括 AVL 樹（“AVL”是發(fā)明者的縮寫）库继，以及紅黑樹，這是 JavaTreeMap所使用的窜醉。

在我們的示例代碼中宪萄，如果我們用 Java 的MyTreeMap替換，隨機字符串和時間戳的運行時間大致相同榨惰。實際上拜英，時間戳運行速度更快，即使它們有序琅催，可能是因為它們花費的時間較少居凶。

總而言之，二叉搜索樹可以以對數(shù)時間實現(xiàn)get和put藤抡，但是只能按照使得樹足夠平衡的順序添加鍵侠碧。自平衡樹通過每次添加新鍵時，進行一些額外的工作來避免這個問題缠黍。

你可以在 http://thinkdast.com/balancing 上閱讀自平衡樹的更多信息弄兜。

13.7 更多練習(xí)

在上一個練習(xí)中，你不必實現(xiàn)remove，但你可能需要嘗試替饿。如果從樹中央刪除節(jié)點语泽，則必須重新排列剩余的節(jié)點，來恢復(fù) BST 的特性盛垦。你可以自己弄清楚如何實現(xiàn)湿弦，或者你可以閱讀 http://thinkdast.com/bstdel 上的說明。

刪除一個節(jié)點并重新平衡一個樹是類似的操作：如果你做這個練習(xí)腾夯，你將更好地了解自平衡樹如何工作。